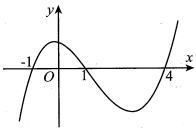
Câu hỏi: Cho hàm số $y=f\left( x \right)$. Hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ. Hàm số $y=f\left( 2-{{e}^{x}} \right)$ đồng biến trên khoảng
A. $\left( 0;\ln 3 \right)$
B. $\left( 1;+\infty \right)$
C. $\left( -1;1 \right)$
D. $\left( -\infty ;0 \right)$

A. $\left( 0;\ln 3 \right)$
B. $\left( 1;+\infty \right)$
C. $\left( -1;1 \right)$
D. $\left( -\infty ;0 \right)$
Ta có ${y}'=-{{e}^{x}}{f}'\left( 2-{{e}^{x}} \right)$.
${y}'=0\Leftrightarrow \left[ \begin{aligned}
& 2-{{e}^{x}}=-1 \\
& 2-{{e}^{x}}=1 \\
& 2-{{e}^{x}}=4 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=0 \\
& x=\ln 3 \\
\end{aligned} \right.$.
Bảng biến thiên

Dựa vào bảng biến thiên suy ra hàm số $y=f\left( 2-{{e}^{x}} \right)$ đồng biến trên các khoảng $\left( -\infty ;0 \right)$ và $\left( \ln 3;+\infty \right)$.
${y}'=0\Leftrightarrow \left[ \begin{aligned}
& 2-{{e}^{x}}=-1 \\
& 2-{{e}^{x}}=1 \\
& 2-{{e}^{x}}=4 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=0 \\
& x=\ln 3 \\
\end{aligned} \right.$.
Bảng biến thiên
Dựa vào bảng biến thiên suy ra hàm số $y=f\left( 2-{{e}^{x}} \right)$ đồng biến trên các khoảng $\left( -\infty ;0 \right)$ và $\left( \ln 3;+\infty \right)$.
Đáp án D.