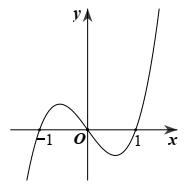
Câu hỏi: Cho hàm số $y=f\left( x \right)$, hàm số ${f}'\left( x \right)={{x}^{3}}+a{{x}^{2}}+bx+c$ $\left( a,b,c\in \mathbb{R} \right)$ có đồ thị như hình vẽ. Hàm số $g\left( x \right)=f\left( {f}'\left( x \right) \right)$ nghịch biến trên khoảng nào dưới đây?
A. $\left( 1;+\infty \right)$.
B. $\left( -\infty ;-2 \right)$.
C. $\left( -1;0 \right)$.
D. $\left( -\dfrac{\sqrt{3}}{3};\dfrac{\sqrt{3}}{3} \right)$.

A. $\left( 1;+\infty \right)$.
B. $\left( -\infty ;-2 \right)$.
C. $\left( -1;0 \right)$.
D. $\left( -\dfrac{\sqrt{3}}{3};\dfrac{\sqrt{3}}{3} \right)$.
Vì các điểm $\left( -1;0 \right)$, $\left( 0;0 \right)$, $\left( 1;0 \right)$ thuộc đồ thị hàm số $y={f}'\left( x \right)$ nên ta có hệ:
$\left\{ \begin{aligned}
& -1+a-b+c=0 \\
& c=0 \\
& 1+a+b+c=0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& a=0 \\
& b=-1 \\
& c=0 \\
\end{aligned} \right.\Rightarrow {f}'\left( x \right)={{x}^{3}}-x\Rightarrow {f}''\left( x \right)=3{{x}^{2}}-1$
Ta có: $g\left( x \right)=f\left( {f}'\left( x \right) \right)\Rightarrow {g}'\left( x \right)={f}'\left( {f}'\left( x \right) \right).{f}''\left( x \right)$
Xét ${g}'\left( x \right)=0\Leftrightarrow {f}'\left( {f}'\left( x \right) \right).{f}''\left( x \right)=0\Leftrightarrow {f}'\left( {{x}^{3}}-x \right).\left( 3{{x}^{2}}-1 \right)=0$
$\Leftrightarrow \left[ \begin{aligned}
& {{x}^{3}}-x=0 \\
& {{x}^{3}}-x=1 \\
& {{x}^{3}}-x=-1 \\
& 3{{x}^{2}}-1=0 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=\pm 1 \\
& x=0 \\
& x=1,325 \\
& x=-1,325 \\
& x=\pm \dfrac{\sqrt{3}}{3} \\
\end{aligned} \right.$
Ta có bảng xét dấu ${g}'\left( x \right)$ như sau:
 Dựa vào bảng biến thiên, suy ra BC nghịch biến trên $\left( -\infty ;-2 \right)$.
Dựa vào bảng biến thiên, suy ra BC nghịch biến trên $\left( -\infty ;-2 \right)$.
$\left\{ \begin{aligned}
& -1+a-b+c=0 \\
& c=0 \\
& 1+a+b+c=0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& a=0 \\
& b=-1 \\
& c=0 \\
\end{aligned} \right.\Rightarrow {f}'\left( x \right)={{x}^{3}}-x\Rightarrow {f}''\left( x \right)=3{{x}^{2}}-1$
Ta có: $g\left( x \right)=f\left( {f}'\left( x \right) \right)\Rightarrow {g}'\left( x \right)={f}'\left( {f}'\left( x \right) \right).{f}''\left( x \right)$
Xét ${g}'\left( x \right)=0\Leftrightarrow {f}'\left( {f}'\left( x \right) \right).{f}''\left( x \right)=0\Leftrightarrow {f}'\left( {{x}^{3}}-x \right).\left( 3{{x}^{2}}-1 \right)=0$
$\Leftrightarrow \left[ \begin{aligned}
& {{x}^{3}}-x=0 \\
& {{x}^{3}}-x=1 \\
& {{x}^{3}}-x=-1 \\
& 3{{x}^{2}}-1=0 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=\pm 1 \\
& x=0 \\
& x=1,325 \\
& x=-1,325 \\
& x=\pm \dfrac{\sqrt{3}}{3} \\
\end{aligned} \right.$
Ta có bảng xét dấu ${g}'\left( x \right)$ như sau:
Đáp án B.