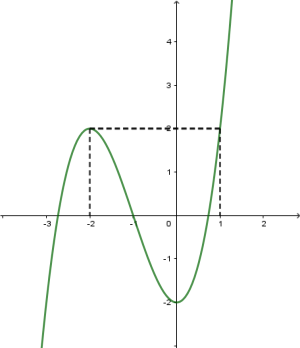
Cho hàm số $y=f\left(x \right)$ có đồ thị như sau Số nghiệm thực của phương trình $f\left(x \right)-2000=0$ là

$f\left(x \right)-2000=0\Leftrightarrow f\left(x \right)=2000$ .
Số nghiệm của phương trình là số giao điểm của đồ thị $y=f\left(x \right)$ và $y=2000$.
Dựa vào đồ thị, ta có đồ thị $y=f\left(x \right)$ cắt đồ thị $y=2000$ tại một điểm thực.
Vậy phương trình có $1$ nghiệm thực .