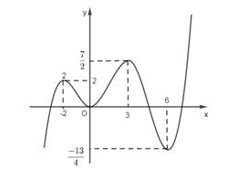
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên $m$ để phương trình $f\left( 2{{x}^{3}}-6x+2 \right)=2m-1$ có 6 nghiệm phân biệt thuộc đoạn $\left[ -1;2 \right]?$
A. 2
B. 3
C. 0
D. 1

A. 2
B. 3
C. 0
D. 1
Đặt $t=2{{x}^{3}}-6x+2\left( * \right)$

Với một giá trị $t\in \left( -2;6 \right]$ thì phương trình $\left( * \right)$ có 2 nghiệm $x\in \left[ -1;2 \right].$
Với một giá trị $t=-2$ thì phương trình $\left( * \right)$ có 1 nghiệm $x\in \left[ -1;2 \right].$
Với một giá trị $t\in \left( -\infty ;-2 \right)\cup \left( 6;+\infty \right)$ thì phương trình $\left( * \right)$ không có nghiệm $x\in \left[ -1;2 \right].$
Phương trình $f\left( 2{{x}^{3}}-6x+2 \right)=2m-1$ có 6 nghiệm phân biệt $x$ thuộc đoạn $\left[ -1;2 \right].$
$\Leftrightarrow $ Phương trình $f\left( t \right)=2m-1$ có 3 nghiệm phân biệt $t\in \left( -2;6 \right].$
$\Leftrightarrow 0<2m-1<2\Leftrightarrow \dfrac{1}{2}<m<\dfrac{3}{2}.$ Vậy có một giá trị nguyên $m=1$ thỏa bài toán.
Với một giá trị $t\in \left( -2;6 \right]$ thì phương trình $\left( * \right)$ có 2 nghiệm $x\in \left[ -1;2 \right].$
Với một giá trị $t=-2$ thì phương trình $\left( * \right)$ có 1 nghiệm $x\in \left[ -1;2 \right].$
Với một giá trị $t\in \left( -\infty ;-2 \right)\cup \left( 6;+\infty \right)$ thì phương trình $\left( * \right)$ không có nghiệm $x\in \left[ -1;2 \right].$
Phương trình $f\left( 2{{x}^{3}}-6x+2 \right)=2m-1$ có 6 nghiệm phân biệt $x$ thuộc đoạn $\left[ -1;2 \right].$
$\Leftrightarrow $ Phương trình $f\left( t \right)=2m-1$ có 3 nghiệm phân biệt $t\in \left( -2;6 \right].$
$\Leftrightarrow 0<2m-1<2\Leftrightarrow \dfrac{1}{2}<m<\dfrac{3}{2}.$ Vậy có một giá trị nguyên $m=1$ thỏa bài toán.
Đáp án D.