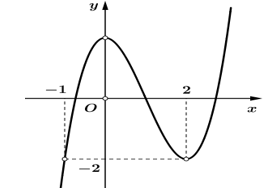
Cho hàm số $y=f\left( x \right)$ có đồ thị như hình dưới đây: Có...

Xét phương trình $f\left( \sqrt{x+4}+\sqrt{4-x}-m \right)+2=0\text{ }\left( * \right)$ trong khoảng $\left( -4;4 \right)$
$\left( * \right)\Leftrightarrow f\left( \sqrt{x+4}+\sqrt{4-x}-m \right)=-2\Leftrightarrow \left[ \begin{aligned}
& \sqrt{x+4}+\sqrt{4-x}-m=2 \\
& \sqrt{x+4}+\sqrt{4-x}-m=-1 \\
\end{aligned} \right.$
$\Leftrightarrow \left[ \begin{aligned}
& \sqrt{x+4}+\sqrt{4-x}=m+2 \\
& \sqrt{x+4}+\sqrt{4-x}=m-1 \\
\end{aligned} \right.$
Xét hàm số $g\left( x \right)=\sqrt{x+4}+\sqrt{4-x}$ trong khoảng $\left( -4;4 \right)$.
Ta có ${g}'\left( x \right)=\dfrac{1}{2\sqrt{x+4}}-\dfrac{1}{2\sqrt{4-x}};{g}'\left( x \right)=0\Leftrightarrow x=0$
Bảng biến thiên
Dựa vào bảng biến thiên, để phương trình đã cho có nghiệm thì $\left[ \begin{aligned}
& 2\sqrt{2}<m+2\le 4 \\
& 2\sqrt{2}<m-1\le 4 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& 2\sqrt{2}-2<m\le 2 \\
& 2\sqrt{2}+1<m\le 5 \\
\end{aligned} \right.$
Mà $m\in \mathbb{Z}$ nên $m\in \left\{ 1;2 \right\}\cup \left\{ 4;5 \right\}$.
Vậy có $4$ giá trị nguyên của $m$ thỏa mãn yêu cầu bài toán.