Google
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có đồ thị như hình bên dưới.
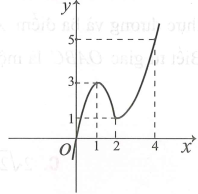
Có bao nhiêu giá trị nguyên của tham số m để phương trình $f\left( \dfrac{6{{\text{x}}^{2}}}{{{x}^{4}}+{{x}^{2}}+1}+2 \right)+1=m$ có nghiệm?
A. 4
B. 2
C. 5
D. 3
Có bao nhiêu giá trị nguyên của tham số m để phương trình $f\left( \dfrac{6{{\text{x}}^{2}}}{{{x}^{4}}+{{x}^{2}}+1}+2 \right)+1=m$ có nghiệm?
A. 4
B. 2
C. 5
D. 3
Cách 1: Phương pháp tự luận truyền thống
Đặt $u=\dfrac{6{{\text{x}}^{2}}}{{{x}^{4}}+{{x}^{2}}+1}+2$.
Ta có ${u}'=\dfrac{-12{{\text{x}}^{5}}+12\text{x}}{{{\left( {{x}^{4}}+{{x}^{2}}+1 \right)}^{2}}}=0\Leftrightarrow \left[ \begin{aligned}
& x=0 \\
& x=\pm 1 \\
\end{aligned} \right.$.
Bài toán trở thành tìm m nguyên để phương trình $f\left( u \right)=m-1$ có nghiệm $u\in \left[ 2;4 \right]$.
Dựa vào đồ thị đề bài cho suy ra $f\left( u \right)=m-1$ có nghiệm $\Leftrightarrow 1\le m-1\le 5\Leftrightarrow 2\le m\le 6$.
Cách 2: Phương pháp ghép trục
$f\left( x \right)$ có cực trị hoành độ $x=1;x=2$.
Đặt $u=\dfrac{6{{\text{x}}^{2}}}{{{x}^{4}}+{{x}^{2}}+1}+2;\text{ {u}'}=\dfrac{-12{{\text{x}}^{5}}+12\text{x}}{{{\left( {{x}^{4}}+{{x}^{2}}+1 \right)}^{2}}}=0\Leftrightarrow \left[ \begin{aligned}
& x=0 \\
& x=\pm 1 \\
\end{aligned} \right.$.
Suy ra $f\left( u \right)=m-1$ có nghiệm $\Leftrightarrow 1\le m-1\le 5\Leftrightarrow 2\le m\le 6$.
Đặt $u=\dfrac{6{{\text{x}}^{2}}}{{{x}^{4}}+{{x}^{2}}+1}+2$.
Ta có ${u}'=\dfrac{-12{{\text{x}}^{5}}+12\text{x}}{{{\left( {{x}^{4}}+{{x}^{2}}+1 \right)}^{2}}}=0\Leftrightarrow \left[ \begin{aligned}
& x=0 \\
& x=\pm 1 \\
\end{aligned} \right.$.
Bài toán trở thành tìm m nguyên để phương trình $f\left( u \right)=m-1$ có nghiệm $u\in \left[ 2;4 \right]$.
Dựa vào đồ thị đề bài cho suy ra $f\left( u \right)=m-1$ có nghiệm $\Leftrightarrow 1\le m-1\le 5\Leftrightarrow 2\le m\le 6$.
Cách 2: Phương pháp ghép trục
$f\left( x \right)$ có cực trị hoành độ $x=1;x=2$.
Đặt $u=\dfrac{6{{\text{x}}^{2}}}{{{x}^{4}}+{{x}^{2}}+1}+2;\text{ {u}'}=\dfrac{-12{{\text{x}}^{5}}+12\text{x}}{{{\left( {{x}^{4}}+{{x}^{2}}+1 \right)}^{2}}}=0\Leftrightarrow \left[ \begin{aligned}
& x=0 \\
& x=\pm 1 \\
\end{aligned} \right.$.
Suy ra $f\left( u \right)=m-1$ có nghiệm $\Leftrightarrow 1\le m-1\le 5\Leftrightarrow 2\le m\le 6$.
| Các bước thực hiện phương pháp ghép trục: Bước 1:Tìm tập xác định của hàm $g=f\left( u(x) \right)$, giả sử ta được tập xác định $D=\left( {{a}_{1}};{{a}_{2}} \right)\cup \left( {{a}_{3}};{{a}_{4}} \right)\cup ...\cup \left( {{a}_{n-1}};{{a}_{n}} \right)$. Ở đây có thể là ${{a}_{1}}\equiv -\infty ;{{\text{a}}_{n}}\equiv +\infty $. Bước 2: Xét sự biến thiên của $u=u\left( x \right)$ và hàm $y=f\left( x \right)$ (Có thể làm gộp trong bước 3 nếu đơn giản). Bước 3: Lập bảng biến thiên tổng hợp xét sự tương quan giữa $\left[ x;u=u\left( x \right) \right]$ và $\left[ u;g=f\left( u \right) \right]$. Bảng này thường có 3 hàng dạng Cụ thể các thành phần trong bảng biến thiên như sau Hàng 1: Xác định các điểm kỳ dị của hàm $u=u\left( x \right)$, sắp xếp các điểm này theo thứ tự tăng dần từ trái qua phải, giả sử: ${{a}_{1}}<{{a}_{2}}<...<{{a}_{n-1}}<{{a}_{n}}$ (xem chú ý 1). Hàng 2: Điền các giá trị ${{u}_{i}}=u\left( {{a}_{i}} \right)$ với $\left( i=\overline{1,...,n} \right)$. Trên mỗi khoảng $\left( {{u}_{i}};{{u}_{i+1}} \right)\overline{i=1,n-1}$ cần bổ sung các điểm kỳ dị ${{b}_{1}};{{b}_{2}};...;{{b}_{k}}$ của hàm $y=f\left( x \right)$. Trên mỗi khoảng $\left( {{u}_{i}};{{u}_{i+1}} \right)\overline{i=1,n-1}$ cần sắp xếp các điểm ${{u}_{i}};{{b}_{k}}$ theo thứ tự chẳng hạn: ${{u}_{i}}<{{b}_{1}}<{{b}_{2}}<...<{{b}_{k}}<{{u}_{i+1}}$ hoặc ${{u}_{i}}>{{b}_{1}}>{{b}_{2}}>...>{{b}_{k}}>{{u}_{i+1}}$ (xem chú ý 2). Hàng 3: Xét chiều biến thiên của hàm $g=f\left( u(x) \right)$ dựa vào bảng biến thiên của hàm $y=f\left( x \right)$ bằng cách hoán đổi: u đóng vai trò của x; $f\left( u \right)$ đóng vai trò của $f\left( x \right)$. Sau khi hoàn thiện bảng biến thiên hàm hợp $g=f\left( u(x) \right)$ ta thấy được hình dạng đồ thị hàm này. Bước 4: Dùng bảng biến thiên hàm hợp $g=f\left( u(x) \right)$ giải quyết các yêu cầu đặt ra trong bài toán và kết luận. Chú ý 1: + Các điểm kỳ dị của $u=u\left( x \right)$ gồm: Điểm biên của tập xác định D và các điểm cực trị của $u=u\left( x \right)$. + Nếu xét hàm $u=\left| u\left( x \right) \right|$ thì trong dòng 1, các điểm kỳ dị còn có nghiệm của phương trình $u\left( x \right)=0$ (là hoành độ giao điểm của $u=u\left( x \right)$ với trục Ox). + Nếu xét hàm $u=\left| u\left( x \right) \right|$ thì trong dòng 1, các điểm kỳ dị còn có số 0 (là hoành độ giao điểm của $u=u\left( x \right)$ với trục Oy). Chú ý 2: + Có thể dùng thêm các mũi tên để thể hiện chiều biến thiên của $u=u\left( x \right)$. + Điểm kỳ dị của $y=f\left( x \right)$ gồm: Các điểm tại đó $f\left( x \right)$ và ${f}'\left( x \right)$ không xác định; các điểm cực trị hàm số $y=f\left( x \right)$. + Nếu xét hàm $g=\left| f\left( u(x) \right) \right|$ thì trong dòng 2, các điểm kỳ dị còn có nghiệm của phương trình $f\left( x \right)=0$ (là hoành độ giao điểm của $u=u\left( x \right)$ với trục Ox). + Nếu xét hàm $g=\left| f\left( u(x) \right) \right|$ thì trong dòng 2, các điểm kỳ dị còn có số 0 (là hoành độ giao điểm của $y=f\left( x \right)$ với trục Oy). |
Đáp án C.