Câu hỏi: Cho hàm số $y=f\left( x \right)$ có đạo hàm và liên tục trên $\mathbb{R}.$ Biết rằng đồ thị hàm số $y=f'\left( x \right)$ như hình dưới đây.
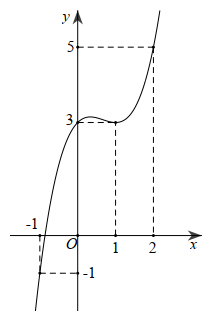
Xét hàm số $g\left( x \right)=f\left( x \right)-{{x}^{2}}-x$ trên $\mathbb{R}.$ Khẳng định nào sau đây là khẳng định sai?
A. $g\left( -1 \right)<g\left( 1 \right).$
B. $g\left( 1 \right)<g\left( 2 \right).$
C. $g\left( 2 \right)<g\left( 1 \right).$
D. $\underset{\mathbb{R}}{\mathop{Min}} \left( g\left( x \right) \right)=\underset{\mathbb{R}}{\mathop{Min}} \left\{ g\left( -1 \right);g\left( 2 \right) \right\}.$

Xét hàm số $g\left( x \right)=f\left( x \right)-{{x}^{2}}-x$ trên $\mathbb{R}.$ Khẳng định nào sau đây là khẳng định sai?
A. $g\left( -1 \right)<g\left( 1 \right).$
B. $g\left( 1 \right)<g\left( 2 \right).$
C. $g\left( 2 \right)<g\left( 1 \right).$
D. $\underset{\mathbb{R}}{\mathop{Min}} \left( g\left( x \right) \right)=\underset{\mathbb{R}}{\mathop{Min}} \left\{ g\left( -1 \right);g\left( 2 \right) \right\}.$
Ta có: $g'\left( x \right)=f'\left( x \right)-2x-1.$
$g'\left( x \right)=0\Leftrightarrow f'\left( x \right)=2x+1.$
Vẽ đồ thị hàm số $y=f'\left( x \right)$ và $y=2x-1$ trên cùng hệ trục tọa độ ta được hình vẽ sau:

Từ đồ thị ta có bảng biến thiên của hàm số $y=g\left( x \right):$

Dựa vào bảng biến thiên ta thấy hàm số $g\left( x \right)$ nghịch biến trên $\left( 1;2 \right)\Rightarrow g\left( 1 \right)>g\left( 2 \right)\Rightarrow $ B sai.
$g'\left( x \right)=0\Leftrightarrow f'\left( x \right)=2x+1.$
Vẽ đồ thị hàm số $y=f'\left( x \right)$ và $y=2x-1$ trên cùng hệ trục tọa độ ta được hình vẽ sau:
Từ đồ thị ta có bảng biến thiên của hàm số $y=g\left( x \right):$
Dựa vào bảng biến thiên ta thấy hàm số $g\left( x \right)$ nghịch biến trên $\left( 1;2 \right)\Rightarrow g\left( 1 \right)>g\left( 2 \right)\Rightarrow $ B sai.
Đáp án B.