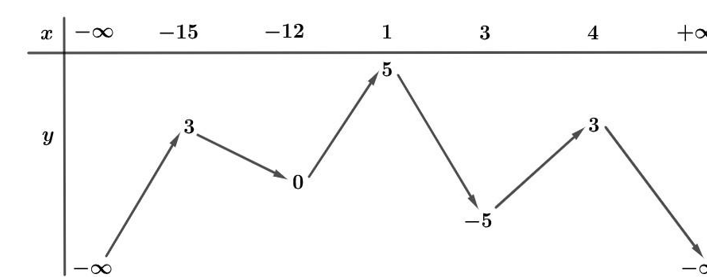
Cho hàm số $y=f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và...

Đặt $u(x)=\left| 2{{x}^{2}}-6x-8 \right|+{{x}^{2}}-13$, khi đó hàm số $u(x)$ không có đạo hàm tại $x=-1;x=4$
$u\left( x \right)=\left\{ \begin{aligned}
& 3{{x}^{2}}-6x-21 khi x\in \left( -\infty ;-1 \right)\cup \left( 4;+\infty \right) \\
& -{{x}^{2}}+6x-5 khi x\in \left( -1;4 \right) \\
\end{aligned} \right.$
${u}'\left( x \right)=\left\{ \begin{aligned}
& 6x-6 khi x\in \left( -\infty ;-1 \right)\cup \left( 4;+\infty \right) \\
& -2x+6 khi x\in \left( -1;4 \right) \\
\end{aligned} \right.$
Ta có ${u}'\left( x \right)=0\Leftrightarrow x=3.$
Bảng biến thiên của hàm số $u\left( x \right)$ :
Ghép trục để có chiều biến thiên của hàm số $f\left( u \right)$ :
Dựa vào bảng biến thiên, hàm số $g\left( x \right)=\left| f\left( u \right) \right|$ có 8 điểm cực đại.