Google
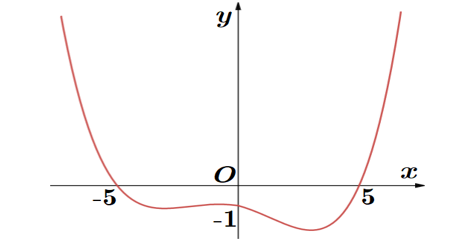
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$. Biết $f\left( -7 \right)<0$ và đồ thị ${f}'\left( x \right)$ như hình vẽ.
Hàm số $g\left( x \right)=\left| 6f\left( -{{x}^{4}}+2{{x}^{2}}-7 \right)-4{{x}^{6}}+12{{x}^{2}} \right|$ có tối đa bao nhiêu điểm cực trị?
A. $5$.
B. $9$.
C. $7$.
D. $3$.
A. $5$.
B. $9$.
C. $7$.
D. $3$.
Xét hàm số $h\left( x \right)=6f\left( -{{x}^{4}}+2{{x}^{2}}-7 \right)-4{{x}^{6}}+12{{x}^{2}}$
$\Rightarrow {h}'\left( x \right)=6\left( -4{{x}^{3}}+4x \right){f}'\left( -{{x}^{4}}+2{{x}^{2}}-7 \right)-24{{x}^{5}}+24x$
$\Leftrightarrow {h}'\left( x \right)=-24x\left( {{x}^{2}}-1 \right){f}'\left( -{{x}^{4}}+2{{x}^{2}}-7 \right)-24x\left( {{x}^{2}}-1 \right)\left( {{x}^{2}}+1 \right)$
$\Leftrightarrow {h}'\left( x \right)=-24x\left( {{x}^{2}}-1 \right)\left[ {f}'\left( -{{x}^{4}}+2{{x}^{2}}-7 \right)+\left( {{x}^{2}}+1 \right) \right]$
Ta có $-{{x}^{4}}+2{{x}^{2}}-7=-{{\left( {{x}^{2}}-1 \right)}^{2}}-6\Rightarrow -{{x}^{4}}+2{{x}^{2}}-7\le -6,\forall t$.
Với $t\le -6$, ${f}'\left( t \right)>0$ nên ${f}'\left( -{{x}^{4}}+2{{x}^{2}}-7 \right)+\left( {{x}^{2}}+1 \right)>0,\forall x$, khi đó:
$\Leftrightarrow {h}'\left( x \right)=0\Leftrightarrow x\left( {{x}^{2}}-1 \right)=0\Leftrightarrow \left[ \begin{matrix}
x=0 \\
x=\pm 1 \\
\end{matrix} \right.$.
Bảng biến thiên:
Từ bảng biến thiên $h\left( 0 \right)=6{f}'\left( -7 \right)<0$ và $h\left( -1 \right)>h\left( 0 \right)$.
Nên phương trình $h\left( x \right)=6f\left( -{{x}^{4}}+2{{x}^{2}}-7 \right)-4{{x}^{6}}+12{{x}^{2}}=0$ có tối đa $4$ nghiệm nên hàm số $g\left( x \right)=\left| h\left( x \right) \right|$ có tối đa $7$ điểm cực trị.
$\Rightarrow {h}'\left( x \right)=6\left( -4{{x}^{3}}+4x \right){f}'\left( -{{x}^{4}}+2{{x}^{2}}-7 \right)-24{{x}^{5}}+24x$
$\Leftrightarrow {h}'\left( x \right)=-24x\left( {{x}^{2}}-1 \right){f}'\left( -{{x}^{4}}+2{{x}^{2}}-7 \right)-24x\left( {{x}^{2}}-1 \right)\left( {{x}^{2}}+1 \right)$
$\Leftrightarrow {h}'\left( x \right)=-24x\left( {{x}^{2}}-1 \right)\left[ {f}'\left( -{{x}^{4}}+2{{x}^{2}}-7 \right)+\left( {{x}^{2}}+1 \right) \right]$
Ta có $-{{x}^{4}}+2{{x}^{2}}-7=-{{\left( {{x}^{2}}-1 \right)}^{2}}-6\Rightarrow -{{x}^{4}}+2{{x}^{2}}-7\le -6,\forall t$.
Với $t\le -6$, ${f}'\left( t \right)>0$ nên ${f}'\left( -{{x}^{4}}+2{{x}^{2}}-7 \right)+\left( {{x}^{2}}+1 \right)>0,\forall x$, khi đó:
$\Leftrightarrow {h}'\left( x \right)=0\Leftrightarrow x\left( {{x}^{2}}-1 \right)=0\Leftrightarrow \left[ \begin{matrix}
x=0 \\
x=\pm 1 \\
\end{matrix} \right.$.
Bảng biến thiên:
Nên phương trình $h\left( x \right)=6f\left( -{{x}^{4}}+2{{x}^{2}}-7 \right)-4{{x}^{6}}+12{{x}^{2}}=0$ có tối đa $4$ nghiệm nên hàm số $g\left( x \right)=\left| h\left( x \right) \right|$ có tối đa $7$ điểm cực trị.
Đáp án C.