Google
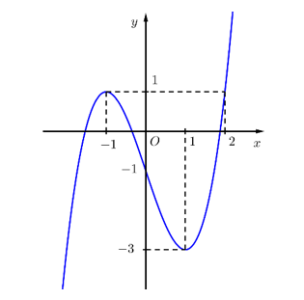
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và có đồ thị hàm số $y={f}'\left( x \right)$ như hình vẽ sau.
Gọi $g\left( x \right)=f\left( x \right)-\dfrac{1}{3}{{x}^{3}}+\dfrac{1}{2}{{x}^{2}}+x-2019$. Biết $g\left( -1 \right)+g\left( 1 \right)>g\left( 0 \right)+g\left( 2 \right)$. Với $x\in \left[ -1; 2 \right]$ thì $g\left( x \right)$ đạt giá trị nhỏ nhất bằng
A. $g\left( 2 \right)$.
B. $g\left( 1 \right)$.
C. $g\left( -1 \right)$.
D. $g\left( 0 \right)$.
A. $g\left( 2 \right)$.
B. $g\left( 1 \right)$.
C. $g\left( -1 \right)$.
D. $g\left( 0 \right)$.
Ta có ${g}'\left( x \right)={f}'\left( x \right)-{{x}^{2}}+x+1={f}'\left( x \right)-\left( {{x}^{2}}-x-1 \right)$
${g}'\left( x \right)=0\Leftrightarrow {f}'\left( x \right)-\left( {{x}^{2}}-x-1 \right)=0$ $\Leftrightarrow {f}'\left( x \right)={{x}^{2}}-x-1$
Dựa vào hình vẽ trên, ta thấy ${f}'\left( x \right)={{x}^{2}}-x-1\Leftrightarrow \left[ \begin{aligned}
& x=-1 \\
& x=0 \\
& x=2 \\
\end{aligned} \right.$.
Bảng biến thiên
Theo giả thiết: $g\left( -1 \right)+g\left( 1 \right)>g\left( 0 \right)+g\left( 2 \right)\Leftrightarrow g\left( -1 \right)-g\left( 2 \right)>g\left( 0 \right)-g\left( 1 \right)>0\Rightarrow g\left( -1 \right)>g\left( 2 \right)$
Vậy $\underset{\left[ -1; 2 \right]}{\mathop{\min }} g\left( x \right)=g\left( 2 \right)$.
▪ Chú ý: Cách khác khi không dùng giả thiết $g\left( -1 \right)+g\left( 1 \right)>g\left( 0 \right)+g\left( 2 \right)$ ở đề bài.
Gọi ${{S}_{1}}$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $y={f}'\left( x \right)$, $y={{x}^{2}}-x-1$, $x=-1, x=0$.
Ta có ${{S}_{1}}=\int\limits_{-1}^{0}{\left| {f}'\left( x \right)-\left( {{x}^{2}}-x-1 \right) \right|\text{d}}x$ $=\int\limits_{-1}^{0}{\left[ {f}'\left( x \right)-\left( {{x}^{2}}-x-1 \right) \right]\text{d}x}$
$=\int\limits_{-1}^{0}{{g}'\left( x \right)\text{d}x}$ $=\left. g\left( x \right) \right|_{-1}^{0}$ $=g\left( 0 \right)-g\left( -1 \right)$.
Gọi ${{S}_{2}}$ là diện tích hình phẳng giới hạn đồ thị hàm số $y={f}'\left( x \right)$, $y={{x}^{2}}-x-1$, $x=0,x=2$.
Ta có ${{S}_{2}}=\int\limits_{0}^{2}{\left| {f}'\left( x \right)-\left( {{x}^{2}}-x-1 \right) \right|\text{d}}x$ $=-\int\limits_{0}^{2}{\left[ {f}'\left( x \right)-\left( {{x}^{2}}-x-1 \right) \right]\text{d}x}$
$=-\int\limits_{0}^{2}{{g}'\left( x \right)\text{d}x}$ $=\left. -g\left( x \right) \right|_{0}^{2}$ $=-g\left( 2 \right)+g\left( 0 \right)$.
Ta có ${{S}_{2}}>{{S}_{1}}$ $\Rightarrow -g\left( 2 \right)+g\left( 0 \right)>g\left( 0 \right)-g\left( -1 \right)$ $\Leftrightarrow -g\left( 2 \right)>-g\left( -1 \right)$ $\Leftrightarrow g\left( 2 \right)<g\left( -1 \right)$.
Vậy $\underset{\left[ -1; 2 \right]}{\mathop{\min }} g\left( x \right)=g\left( 2 \right)$.
${g}'\left( x \right)=0\Leftrightarrow {f}'\left( x \right)-\left( {{x}^{2}}-x-1 \right)=0$ $\Leftrightarrow {f}'\left( x \right)={{x}^{2}}-x-1$
& x=-1 \\
& x=0 \\
& x=2 \\
\end{aligned} \right.$.
Bảng biến thiên
Vậy $\underset{\left[ -1; 2 \right]}{\mathop{\min }} g\left( x \right)=g\left( 2 \right)$.
▪ Chú ý: Cách khác khi không dùng giả thiết $g\left( -1 \right)+g\left( 1 \right)>g\left( 0 \right)+g\left( 2 \right)$ ở đề bài.
Ta có ${{S}_{1}}=\int\limits_{-1}^{0}{\left| {f}'\left( x \right)-\left( {{x}^{2}}-x-1 \right) \right|\text{d}}x$ $=\int\limits_{-1}^{0}{\left[ {f}'\left( x \right)-\left( {{x}^{2}}-x-1 \right) \right]\text{d}x}$
$=\int\limits_{-1}^{0}{{g}'\left( x \right)\text{d}x}$ $=\left. g\left( x \right) \right|_{-1}^{0}$ $=g\left( 0 \right)-g\left( -1 \right)$.
Gọi ${{S}_{2}}$ là diện tích hình phẳng giới hạn đồ thị hàm số $y={f}'\left( x \right)$, $y={{x}^{2}}-x-1$, $x=0,x=2$.
Ta có ${{S}_{2}}=\int\limits_{0}^{2}{\left| {f}'\left( x \right)-\left( {{x}^{2}}-x-1 \right) \right|\text{d}}x$ $=-\int\limits_{0}^{2}{\left[ {f}'\left( x \right)-\left( {{x}^{2}}-x-1 \right) \right]\text{d}x}$
$=-\int\limits_{0}^{2}{{g}'\left( x \right)\text{d}x}$ $=\left. -g\left( x \right) \right|_{0}^{2}$ $=-g\left( 2 \right)+g\left( 0 \right)$.
Ta có ${{S}_{2}}>{{S}_{1}}$ $\Rightarrow -g\left( 2 \right)+g\left( 0 \right)>g\left( 0 \right)-g\left( -1 \right)$ $\Leftrightarrow -g\left( 2 \right)>-g\left( -1 \right)$ $\Leftrightarrow g\left( 2 \right)<g\left( -1 \right)$.
Vậy $\underset{\left[ -1; 2 \right]}{\mathop{\min }} g\left( x \right)=g\left( 2 \right)$.
Đáp án A.