Google
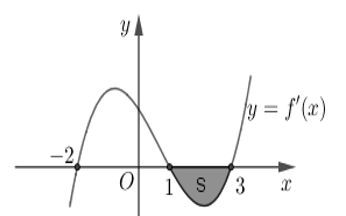
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\left[ -2;3 \right]$ và ${f}'\left( x \right)$ có đồ thị như hình vẽ sau:
Biết $\int\limits_{-2}^{1}{{f}'\left( x \right)\text{d}x}=3$ và diện tích $S=\dfrac{5}{3}$. Giá trị $f\left( 3 \right)-f\left( -2 \right)$ bằng
A. $-\dfrac{14}{3}\cdot $
B. $\dfrac{4}{3}\cdot $
C. $-\dfrac{4}{3}\cdot $
D. $\dfrac{14}{3}\cdot $
A. $-\dfrac{14}{3}\cdot $
B. $\dfrac{4}{3}\cdot $
C. $-\dfrac{4}{3}\cdot $
D. $\dfrac{14}{3}\cdot $
Diện tích $S=\int\limits_{1}^{3}{\left| f\left( x \right) \right|\text{d}x}=\dfrac{5}{3}\Rightarrow S=-\int\limits_{1}^{3}{f\left( x \right)\text{d}x}=\dfrac{5}{3}\Rightarrow \int\limits_{1}^{3}{f\left( x \right)\text{d}x}=-\dfrac{5}{3}$.
Ta có $\int\limits_{-2}^{3}{{f}'\left( x \right)\text{d}x}=\int\limits_{-2}^{1}{{f}'\left( x \right)\text{d}x}+\int\limits_{1}^{3}{{f}'\left( x \right)\text{d}x}\Rightarrow f\left( 3 \right)-f\left( -2 \right)=3-\dfrac{5}{3}=\dfrac{4}{3}$.
Ta có $\int\limits_{-2}^{3}{{f}'\left( x \right)\text{d}x}=\int\limits_{-2}^{1}{{f}'\left( x \right)\text{d}x}+\int\limits_{1}^{3}{{f}'\left( x \right)\text{d}x}\Rightarrow f\left( 3 \right)-f\left( -2 \right)=3-\dfrac{5}{3}=\dfrac{4}{3}$.
Đáp án B.