Google
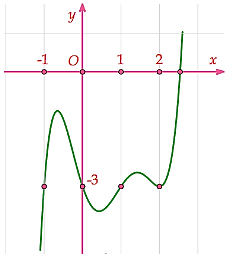
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có đạo hàm ${f}'\left( x \right)$. Đồ thị của hàm số $y={f}'\left( x \right)$ như hình vẽ.
Giá trị lớn nhất của hàm số $g\left( x \right)=f\left( 3x \right)+9x$ trên đoạn $\left[ -\dfrac{1}{3};\dfrac{1}{3} \right]$ là
A. $f\left( 0 \right)$.
B. $f\left( 1 \right)+2$.
C. $f\left( \dfrac{1}{3} \right)$.
D. $f\left( 1 \right)$.
Đặt $t=3x\xrightarrow{x\in \left[ -\dfrac{1}{3};\dfrac{1}{3} \right]}t\in \left[ -1;1 \right]$
Xét hàm số $y=f\left( t \right)+3t,t\in \left[ -1;1 \right]$ có ${y}'={f}'\left( t \right)+3$
Cho ${y}'=0\Leftrightarrow {f}'\left( x \right)=-3\Leftrightarrow \left[ \begin{aligned}
& t=-1 \\
& t=0 \\
& t=1 \\
& t=2(loai) \\
\end{aligned} \right.$
$y\left( -1 \right)=f\left( -1 \right)-3;y\left( 1 \right)=f\left( 1 \right)+3;y\left( 0 \right)=f\left( 0 \right)$
Vậy $\underset{\left[ -1;1 \right]}{\mathop{\max }} y=f\left( 0 \right)$
A. $f\left( 0 \right)$.
B. $f\left( 1 \right)+2$.
C. $f\left( \dfrac{1}{3} \right)$.
D. $f\left( 1 \right)$.
Xét hàm số $y=f\left( t \right)+3t,t\in \left[ -1;1 \right]$ có ${y}'={f}'\left( t \right)+3$
Cho ${y}'=0\Leftrightarrow {f}'\left( x \right)=-3\Leftrightarrow \left[ \begin{aligned}
& t=-1 \\
& t=0 \\
& t=1 \\
& t=2(loai) \\
\end{aligned} \right.$
$y\left( -1 \right)=f\left( -1 \right)-3;y\left( 1 \right)=f\left( 1 \right)+3;y\left( 0 \right)=f\left( 0 \right)$
Đáp án A.