Câu hỏi: Cho hàm số $y=f\left(x \right)$ có bảng xét dấu của đạo hàm như sau
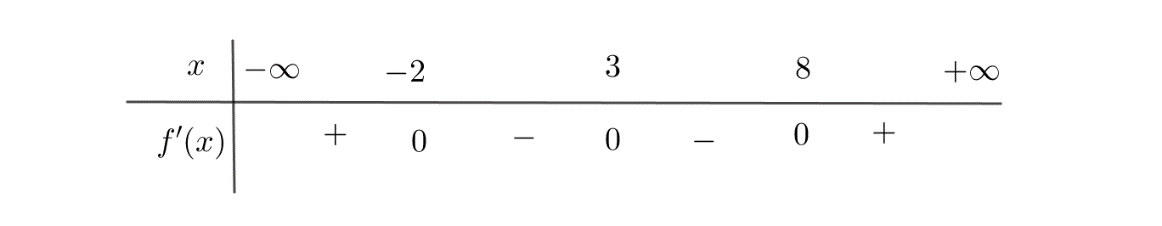
Số giá trị nguyên của tham số $m$ để hàm số $y=f\left({{x}^{2}}+4x+m \right)$ nghịch biến trên $\left(-1; 1 \right)$ là
A. $3$.
B. $0$.
C. $1$.
D. $2$.
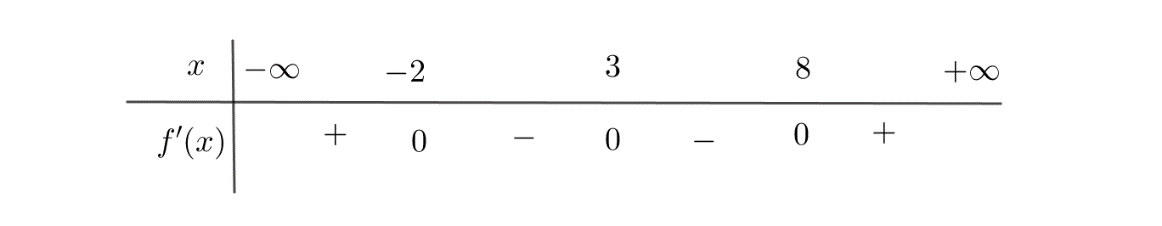
Số giá trị nguyên của tham số $m$ để hàm số $y=f\left({{x}^{2}}+4x+m \right)$ nghịch biến trên $\left(-1; 1 \right)$ là
A. $3$.
B. $0$.
C. $1$.
D. $2$.
Hàm số $y=f\left( {{x}^{2}}+4x+m \right)$ nghịch biến trên $\left( -1 ; 1 \right)$
$\Leftrightarrow {y}'=\left( 2x+4 \right).{f}'\left( {{x}^{2}}+4x+m \right)\le 0, \forall x\in \left( -1 ; 1 \right)$
$\Leftrightarrow {f}'\left( {{x}^{2}}+4x+m \right)\le 0, \forall x\in \left( -1 ; 1 \right)$ (*)
Đặt $t={{x}^{2}}+4x+m$
BBT

(*) $\Leftrightarrow {f}'\left( t \right)\le 0, \forall t\in \left( m-3 ; m+5 \right)$
$\Leftrightarrow -2\le m-3<m+5\le 8$ $\Leftrightarrow 1\le m\le 3$ mà $m\in \mathbb{Z}$ nên $m\in \left\{ 1 ; 2 ; 3 \right\}$.
Vậy có 3 giá trị nguyên của tham số $m$ thỏa ycbt.
$\Leftrightarrow {y}'=\left( 2x+4 \right).{f}'\left( {{x}^{2}}+4x+m \right)\le 0, \forall x\in \left( -1 ; 1 \right)$
$\Leftrightarrow {f}'\left( {{x}^{2}}+4x+m \right)\le 0, \forall x\in \left( -1 ; 1 \right)$ (*)
Đặt $t={{x}^{2}}+4x+m$
BBT
(*) $\Leftrightarrow {f}'\left( t \right)\le 0, \forall t\in \left( m-3 ; m+5 \right)$
$\Leftrightarrow -2\le m-3<m+5\le 8$ $\Leftrightarrow 1\le m\le 3$ mà $m\in \mathbb{Z}$ nên $m\in \left\{ 1 ; 2 ; 3 \right\}$.
Vậy có 3 giá trị nguyên của tham số $m$ thỏa ycbt.
Đáp án A.