Google
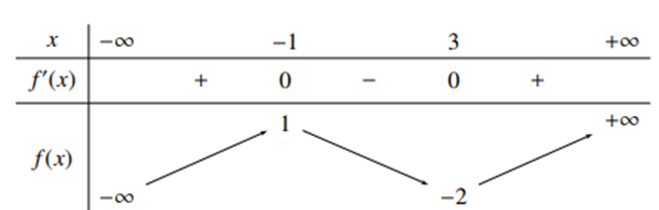
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:
Gọi $M,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=f\left( 2\cos x+1 \right)$. Tính $M+m$.
A. $-2$
B. 1
C. $-1$
D. 0
A. $-2$
B. 1
C. $-1$
D. 0
Đặt $t=2\cos x+1 \left( t\in \left[ -1 ; 3 \right] \right)$.
Ta có : $M=\underset{\mathbb{R}}{\mathop{\text{max}}} y=\underset{\left[ -1 ; 3 \right]}{\mathop{\text{max}}} f\left( t \right)=1$ ; $m=\underset{\mathbb{R}}{\mathop{\text{min}}} y=\underset{\left[ -1 ; 3 \right]}{\mathop{\text{min}}} f\left( t \right)=-2$. Suy ra $M+m=-1$.
Ta có : $M=\underset{\mathbb{R}}{\mathop{\text{max}}} y=\underset{\left[ -1 ; 3 \right]}{\mathop{\text{max}}} f\left( t \right)=1$ ; $m=\underset{\mathbb{R}}{\mathop{\text{min}}} y=\underset{\left[ -1 ; 3 \right]}{\mathop{\text{min}}} f\left( t \right)=-2$. Suy ra $M+m=-1$.
Đáp án C.