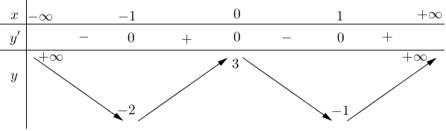
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình bên. Phương trình $2f\left( \dfrac{\sin x+\cos x}{\sqrt{2}} \right)+3=0$ có bao...

Phương pháp:
- Đặt $t=\dfrac{\sin x+\cos x}{\sqrt{2}},$ tìm điều kiện của $t$ ứng với $x\in \left[ \dfrac{-3\pi }{4};\dfrac{7\pi }{4} \right].$
- Sử dụng tương giao để tìm số nghiệm của phương trình.
Cách giải:
Đặt $t=\dfrac{\sin x+\cos x}{\sqrt{2}}=\dfrac{\sqrt{2}\sin \left( x+\dfrac{\pi }{4} \right)}{\sqrt{2}}=\sin \left( x+\dfrac{\pi }{4} \right).$
Với $x\in \left[ \dfrac{-3\pi }{4};\dfrac{7\pi }{4} \right]\Rightarrow x+\dfrac{\pi }{4}\in \left[ -\dfrac{\pi }{2};2\pi \right]\Rightarrow t\in \left[ -1;1 \right].$
Khi đó phương trình trở thành $2f\left( t \right)+3=0\Leftrightarrow f\left( t \right)=-\dfrac{3}{2}.$
Dựa vào BBT ta thấy đường thẳng $y=-\dfrac{3}{2}$ cắt đồ thị hàm số $y=f\left( t \right)$ tại 2 điểm phân biệt $\left[ \begin{aligned}
& x=t<-1 \\
& x=t\in \left( -1;0 \right) \\
\end{aligned} \right..$
$\Rightarrow f\left( t \right)=-\dfrac{3}{2}\Leftrightarrow \left[ \begin{aligned}
& t=a<-1 \\
& t=b\in \left( -1;0 \right) \\
\end{aligned} \right..$
Ta có đồ thị hàm số $t=\sin \left( x+\dfrac{\pi }{4} \right)$ trên $\left[ -\dfrac{\pi }{2};2\pi \right]$ như sau:

Dựa vào đồ thị ta thấy, phương trình $t=a$ vô nghiệm, phương trình $t=b$ có 3 nghiệm phân biệt.