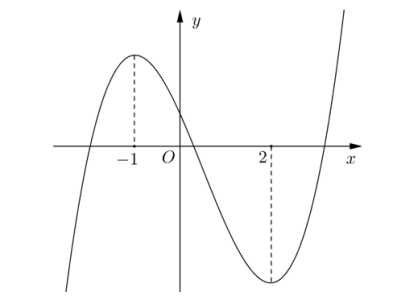
Cho hàm số $y=f\left( 3-5x \right)$ xác định và liên tục trên...

Dựa vào đồ thị ta có: ${y}'=-5.{f}'\left( 3-5x \right)=\left( x+1 \right)\left( x-2 \right)$ $\Rightarrow {f}'\left( 3-5x \right)=-\dfrac{1}{5}\left( x+1 \right)\left( x-2 \right)$.
$\Rightarrow {f}'\left( 3-5u \right)=-\dfrac{1}{5}\left( u+1 \right)\left( u-2 \right)$.
Đặt $3-5u=x$, ta có ${f}'\left( x \right)=-\dfrac{1}{5}\left( \dfrac{3-x}{5}+1 \right)\left( \dfrac{3-x}{5}-2 \right)=\dfrac{1}{125}\left( 8-x \right)\left( x+7 \right)$.
Ta có: $g\left( x \right)=f\left( {{x}^{3}}+m \right)$, ${g}'\left( x \right)=3{{x}^{2}}.{f}'\left( {{x}^{3}}+m \right)$
${g}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=0 \\
& {f}'\left( {{x}^{3}}+m \right)=0 \\
\end{aligned} \right. $, trong đó $ x=0$ là nghiệm bội chẵn.
Xét phương trình ${f}'\left( {{x}^{3}}+m \right)=0\Leftrightarrow \left[ \begin{aligned}
& {{x}^{3}}+m=-7 \\
& {{x}^{3}}+m=8 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=\sqrt[3]{-m-7} \\
& x=\sqrt[3]{-m+8} \\
\end{aligned} \right.$.
Các nghiệm $x=\sqrt[3]{-m-7}, x=\sqrt[3]{-m+8}$ là các nghiệm bội lẻ nên hàm số $g\left( x \right)=f\left( {{x}^{3}}+m \right)$ có 2 điểm cực trị là $x=\sqrt[3]{-m-7}, x=\sqrt[3]{-m+8}$.
Đồ thị hàm số $g\left( x \right)=f\left( {{x}^{3}}+m \right)$ có đúng 2 điểm cực trị nằm về 2 phía của đường thẳng $x=2$ khi $\left\{ \begin{aligned}
& \sqrt[3]{-m-7}<2 \\
& \sqrt[3]{-m+8}>2 \\
\end{aligned} \right.\Leftrightarrow -15<m<0$.
Do $m$ nguyên nên $m\in \left\{ -14; -13;...; -1 \right\}$ hay $S=\left\{ -14; -13;...; -1 \right\}$.
Vậy tổng các phần tử của tập hợp $S$ bằng $-105$.