T
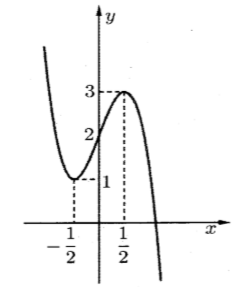
Cho hàm số
Cho hàm số
- Tác giả The Knowledge
- Creation date
-
- Tags
- trắc nghiệm toán 12