Cho hàm số $f(x)={{x}^{3}}-3{{x}^{2}}+1$ và $g(x)=f\left( \left|...

Ta có: $f(x)={{x}^{3}}-3{{x}^{2}}+1$ và $g(x)=f\left( \left| f(x) \right|-m \right);f(-1)=-3;f(1)=-1;$
Suy ra $g'(x)={{\left( \left| f(x) \right| \right)}^{\prime }}.{f}'\left( \left| f(x) \right|-m \right)=\dfrac{f(x){f}'(x)}{\sqrt{{{f}^{2}}(x)}}.{f}'\left( \left| f(x) \right|-m \right)=0$
$\Leftrightarrow \left[ \begin{aligned}
& x=0;x=2 \\
& \left| f(x) \right|-m=0 \\
& \left| f(x) \right|-m=2 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=0;x=2 \\
& \left| f(x) \right|=m \\
& \left| f(x) \right|=m+2 \\
\end{aligned} \right.$(*)
Mặt khác, $f\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x={{a}_{1}}\in \left( -1;0 \right)\approx -0.53, \\
& x={{b}_{1}}\in \left( 0;1 \right)\approx 0.65 \\
& x={{c}_{1}}\in \left( 2;3 \right)\approx 2.8 \\
\end{aligned} \right. $ nên các điểm $ x={{a}_{1}};x={{b}_{1}};x={{c}_{1}} $ là các điểm cực trị của $ g\left( x \right)$.
Để hai điểm $x=-1;x=1$ là hai điểm cực trị của hàm số $y=g(x)$ thì hai giá trị $x$ đó phải là nghiệm của hệ phương trình: $\left\{ \begin{aligned}
& \left[ \begin{aligned}
& \left| f(x) \right|=m \\
& \left| f(x) \right|=m+2 \\
\end{aligned} \right. \\
& \left| f(-1) \right|=3;\left| f(1) \right|=1; \\
\end{aligned} \right.\Rightarrow \left[ \begin{aligned}
& m=3 \\
& m=1 \\
& m+2=3 \\
& m+2=1 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& m=-1 \\
& m=1 \\
& m=3 \\
\end{aligned} \right.$.
Với $m=3$ thì suy ra $\left[ \begin{aligned}
& \left| f(x) \right|=3 \\
& \left| f(x) \right|=5 \\
\end{aligned} \right. $, tới đây ta nhận thấy hệ phương trình trên không có nghiệm $ x=-1;x=1$nên ta loại
Với $m=-1$ thì suy ra $\left[ \begin{aligned}
& \left| f(x) \right|=-1 \\
& \left| f(x) \right|=1 \\
\end{aligned} \right. $, tới đây ta nhận thấy hệ phương trình kia không có nghiệm $ x=-1$nên ta loại
Với $m=1$ thì suy ra $\left[ \begin{aligned}
& \left| f(x) \right|=1 \\
& \left| f(x) \right|=3 \\
\end{aligned} \right. $. Do hệ phương trình này có hai nghiệm $ x=-1;x=1$ nên hệ phương trình tương đương với (dựa vào đồ thị hình bên)
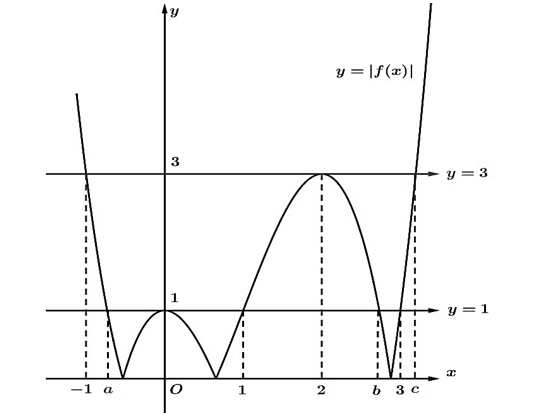Suy ra $\left[ \begin{aligned}
& x=a\in \left( -1;0 \right) \\
& x=0 \\
& x=1 \\
& x=b\in \left( 2;3 \right) \\
& x=3 \\
& x=-1 \\
& x=2 \\
& x=c\in \left( 3,4 \right) \\
\end{aligned} \right. $. Do $ x=0,x=2 $ là nghiệm bội chẵn nên $ \left[ \begin{aligned}
& x=a\in \left( -1;0 \right) \\
& x=1 \\
& x=b\in \left( 2;3 \right) \\
& x=3 \\
& x=-1 \\
& x=c\in \left( 3,4 \right) \\
\end{aligned} \right.$ là 6 nghiệm bội lẻ.
Như vậy hệ phương trình (*) có tổng cộng 11 nghiệm tương đương với hàm số $y=g(x)$ có 11 điểm cực trị thỏa đề bài.