Google
Câu hỏi: Cho hàm số $f\left( x \right)=-{{x}^{4}}-\left( 5-{{m}^{2}} \right)x+2023$ và $g\left( x \right)=-{{x}^{3}}+5{{x}^{2}}-2022x+2023$. Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $h\left( x \right)=g\left[ f\left( x \right) \right]$ đồng biến trên khoảng $\left( 1 ; +\infty \right)$ ?
A. $7$.
B. $5$.
C. $6$.
D. $8$.
A. $7$.
B. $5$.
C. $6$.
D. $8$.
${f}'\left( x \right)=-4{{x}^{3}}-\left( 5-{{m}^{2}} \right)$
${g}'\left( x \right)=-3{{x}^{3}}+10{{x}^{2}}-2022<0 \forall x\in \left( 1;+\infty \right)$
${h}'\left( x \right)={{\left( g\left[ f\left( x \right) \right] \right)}^{\prime }}={f}'\left( x \right).{g}'\left[ f\left( x \right) \right]$
Để hàm số đồng biến trên khoảng $\left( 1 ; +\infty \right)$ thì ${h}'\left( x \right)>0;\forall x\in \left( 1 ; +\infty \right)$
$\begin{aligned}
& \Rightarrow {f}'\left( x \right).{g}'\left[ f\left( x \right) \right]>0;\forall x\in \left( 1 ; +\infty \right) \\
& \Rightarrow {f}'\left( x \right)<0;\forall x\in \left( 1 ; +\infty \right) \\
& \Rightarrow -4{{x}^{3}}-\left( 5-{{m}^{2}} \right)<0;\forall x\in \left( 1 ; +\infty \right) \\
& \Rightarrow -4{{x}^{3}}<\left( 5-{{m}^{2}} \right);\forall x\in \left( 1 ; +\infty \right) \\
\end{aligned}$
Xét hàm: $K\left( x \right)=-4{{x}^{3}}\Rightarrow {K}'\left( x \right)=-12{{x}^{2}}$
${K}'\left( x \right)=0\Leftrightarrow -12{{x}^{2}}=0\Leftrightarrow x=0$
Bảng xét dấu
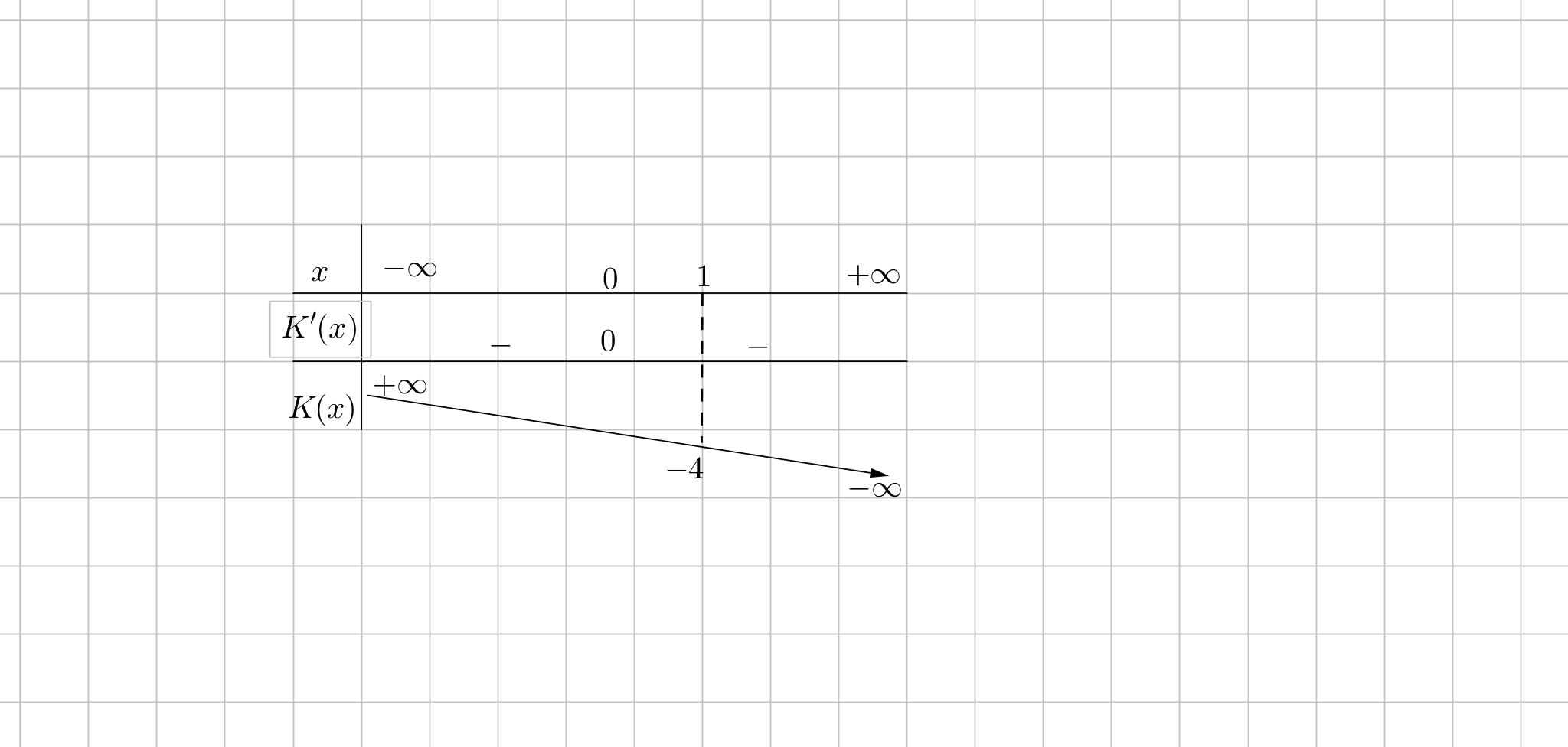Dựa vào bảng biến thiên
$-4{{x}^{3}}<\left( 5-{{m}^{2}} \right);\forall x\in \left( 1 ; +\infty \right)$ $\Leftrightarrow 5-{{m}^{2}}\ge -4\Leftrightarrow {{m}^{2}}\le 9\Leftrightarrow -3\le m\le 3$.
Vậy có $7$ giá trị nguyên của $m$ thỏa mãn bài toán.
${g}'\left( x \right)=-3{{x}^{3}}+10{{x}^{2}}-2022<0 \forall x\in \left( 1;+\infty \right)$
${h}'\left( x \right)={{\left( g\left[ f\left( x \right) \right] \right)}^{\prime }}={f}'\left( x \right).{g}'\left[ f\left( x \right) \right]$
Để hàm số đồng biến trên khoảng $\left( 1 ; +\infty \right)$ thì ${h}'\left( x \right)>0;\forall x\in \left( 1 ; +\infty \right)$
$\begin{aligned}
& \Rightarrow {f}'\left( x \right).{g}'\left[ f\left( x \right) \right]>0;\forall x\in \left( 1 ; +\infty \right) \\
& \Rightarrow {f}'\left( x \right)<0;\forall x\in \left( 1 ; +\infty \right) \\
& \Rightarrow -4{{x}^{3}}-\left( 5-{{m}^{2}} \right)<0;\forall x\in \left( 1 ; +\infty \right) \\
& \Rightarrow -4{{x}^{3}}<\left( 5-{{m}^{2}} \right);\forall x\in \left( 1 ; +\infty \right) \\
\end{aligned}$
Xét hàm: $K\left( x \right)=-4{{x}^{3}}\Rightarrow {K}'\left( x \right)=-12{{x}^{2}}$
${K}'\left( x \right)=0\Leftrightarrow -12{{x}^{2}}=0\Leftrightarrow x=0$
Bảng xét dấu
$-4{{x}^{3}}<\left( 5-{{m}^{2}} \right);\forall x\in \left( 1 ; +\infty \right)$ $\Leftrightarrow 5-{{m}^{2}}\ge -4\Leftrightarrow {{m}^{2}}\le 9\Leftrightarrow -3\le m\le 3$.
Vậy có $7$ giá trị nguyên của $m$ thỏa mãn bài toán.
Đáp án A.
