Google
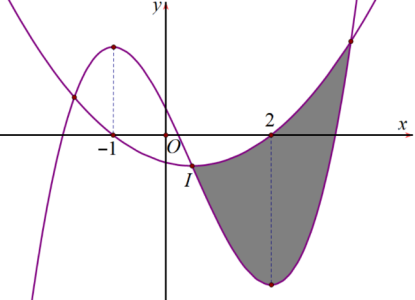
Câu hỏi: Cho hàm số $f\left( x \right)$ với đồ thị là Parabol đỉnh $I$ có tung độ bằng $-\dfrac{7}{12}$ và hàm số bậc ba $g\left( x \right)$. Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ ${{x}_{1}},{{x}_{2}},{{x}_{3}}$ thoả mãn $18{{x}_{1}}{{x}_{2}}{{x}_{3}}=-55$ (hình vẽ).
Diện tích miền tô đậm gần số nào nhất trong các số sau đây?
A. 5,7.
B. 5,9.
C. 6,1.
D. 6,3.
Hàm số $g\left( x \right)$ đạt cực trị tại $x=-1,x=2$ nên
$g'\left( x \right)=a\left( x+1 \right)\left( x-2 \right)\Rightarrow g\left( x \right)=a\left( \dfrac{{{x}^{3}}}{3}-\dfrac{{{x}^{2}}}{2}-2x \right)+b$
Đồ thị hàm số $g\left( x \right)$ đi qua $I$ nên $g\left( \dfrac{1}{2} \right)=-\dfrac{7}{12}\Leftrightarrow -\dfrac{7}{12}=-\dfrac{13}{12}a+b,$ $\left( 1 \right)$.
Phương trình hoành độ giao điểm: $f\left( x \right)=g\left( x \right)\Leftrightarrow a\left( \dfrac{{{x}^{3}}}{3}-\dfrac{{{x}^{2}}}{2}-2x \right)+b=\dfrac{7}{27}\left( x+1 \right)\left( x-2 \right)$
Theo định lý viet ta có: $18{{x}_{1}}{{x}_{2}}{{x}_{3}}=-55\Leftrightarrow 18.\dfrac{b+\dfrac{14}{27}}{\dfrac{a}{3}}=-55\Rightarrow 18b+\dfrac{28}{3}=-\dfrac{55a}{3},$ $\left( 2 \right)$
Từ $\left( 1 \right)$, $\left( 2 \right)$ ta được $a=1,b=\dfrac{1}{2}\Rightarrow g\left( x \right)=\dfrac{{{x}^{3}}}{3}-\dfrac{{{x}^{2}}}{2}-2x+\dfrac{1}{2}$. Từ đó suy ra diện tích miền tô đậm sấp sỉ 5,7.
A. 5,7.
B. 5,9.
C. 6,1.
D. 6,3.
Dễ thấy $I\left( \dfrac{1}{2},-\dfrac{7}{12} \right)$ và $f\left( x \right)=\dfrac{7}{27}\left( x+1 \right)\left( x-2 \right)$.Hàm số $g\left( x \right)$ đạt cực trị tại $x=-1,x=2$ nên
$g'\left( x \right)=a\left( x+1 \right)\left( x-2 \right)\Rightarrow g\left( x \right)=a\left( \dfrac{{{x}^{3}}}{3}-\dfrac{{{x}^{2}}}{2}-2x \right)+b$
Đồ thị hàm số $g\left( x \right)$ đi qua $I$ nên $g\left( \dfrac{1}{2} \right)=-\dfrac{7}{12}\Leftrightarrow -\dfrac{7}{12}=-\dfrac{13}{12}a+b,$ $\left( 1 \right)$.
Phương trình hoành độ giao điểm: $f\left( x \right)=g\left( x \right)\Leftrightarrow a\left( \dfrac{{{x}^{3}}}{3}-\dfrac{{{x}^{2}}}{2}-2x \right)+b=\dfrac{7}{27}\left( x+1 \right)\left( x-2 \right)$
Theo định lý viet ta có: $18{{x}_{1}}{{x}_{2}}{{x}_{3}}=-55\Leftrightarrow 18.\dfrac{b+\dfrac{14}{27}}{\dfrac{a}{3}}=-55\Rightarrow 18b+\dfrac{28}{3}=-\dfrac{55a}{3},$ $\left( 2 \right)$
Từ $\left( 1 \right)$, $\left( 2 \right)$ ta được $a=1,b=\dfrac{1}{2}\Rightarrow g\left( x \right)=\dfrac{{{x}^{3}}}{3}-\dfrac{{{x}^{2}}}{2}-2x+\dfrac{1}{2}$. Từ đó suy ra diện tích miền tô đậm sấp sỉ 5,7.
Đáp án A.