Google
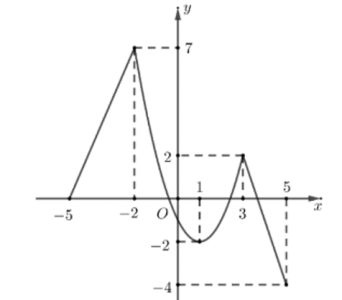
Câu hỏi: Cho hàm số $f\left( x \right)$ và đồ thị hàm số ${f}'\left( x \right)$ liên tục trên $\mathbb{R}$ như hình bên dưới.
Có bao nhiêu giá trị nguyên của tham số $m\in \left( -10;10 \right)$ để hàm số $y=f\left( 2x-1 \right)-2\ln \left( 1+{{x}^{2}} \right)-2mx$ đồng biến trên khoảng $\left( -1;2 \right)$ ?
A. $6$.
B. $7$.
C. $5$.
D. $8$.
A. $6$.
B. $7$.
C. $5$.
D. $8$.
Ta có ${y}'=2{f}'\left( 2x-1 \right)-\dfrac{4x}{1+{{x}^{2}}}-2m$.
Hàm số đã cho đồng biến trên khoảng $\left( -1;2 \right)$ khi ${y}'\ge 0,\forall x\in \left( -1;2 \right)$
$\Rightarrow m\le {f}'\left( 2x-1 \right)-\dfrac{2x}{1+{{x}^{2}}},\forall x\in \left( -1;2 \right)$.
Đặt $g\left( x \right)=-\dfrac{2x}{1+{{x}^{2}}}$ có ${g}'\left( x \right)=\dfrac{2\left( {{x}^{2}}-1 \right)}{{{\left( 1+{{x}^{2}} \right)}^{2}}}$
và $h\left( x \right)={f}'\left( 2x-1 \right)-\dfrac{2x}{1+{{x}^{2}}}$.
Với $a>0$ ta có bảng biến thiên sau
Dễ thấy $\underset{\left( -1;2 \right)}{\mathop{\min }} h\left( x \right)=h\left( 1 \right)=-3$.
$\Rightarrow m\le h\left( x \right),\forall x\in \left( -1;2 \right)\Leftrightarrow m\le -3$.
Vì $m\in \left( -10;10 \right)$ nên $m\in \left\{ -9;-8;-7;-6;-5;-4;-3 \right\}$.
Hàm số đã cho đồng biến trên khoảng $\left( -1;2 \right)$ khi ${y}'\ge 0,\forall x\in \left( -1;2 \right)$
$\Rightarrow m\le {f}'\left( 2x-1 \right)-\dfrac{2x}{1+{{x}^{2}}},\forall x\in \left( -1;2 \right)$.
Đặt $g\left( x \right)=-\dfrac{2x}{1+{{x}^{2}}}$ có ${g}'\left( x \right)=\dfrac{2\left( {{x}^{2}}-1 \right)}{{{\left( 1+{{x}^{2}} \right)}^{2}}}$
và $h\left( x \right)={f}'\left( 2x-1 \right)-\dfrac{2x}{1+{{x}^{2}}}$.
Với $a>0$ ta có bảng biến thiên sau
Dễ thấy $\underset{\left( -1;2 \right)}{\mathop{\min }} h\left( x \right)=h\left( 1 \right)=-3$.
$\Rightarrow m\le h\left( x \right),\forall x\in \left( -1;2 \right)\Leftrightarrow m\le -3$.
Vì $m\in \left( -10;10 \right)$ nên $m\in \left\{ -9;-8;-7;-6;-5;-4;-3 \right\}$.
Đáp án B.