Google
Câu hỏi: Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ bên:
Số nghiệm thuộc đoạn $\left[ -\pi ;3\pi \right]$ của phương trình $f\left( -2\cos 2x+1 \right)=\dfrac{1}{2{{\sin }^{2}}x}$ là
A. $24$.
B. $12$.
C. $16$.
D. $18$.
A. $24$.
B. $12$.
C. $16$.
D. $18$.
Đặt $t=-2\cos 2x+1\in \left[ -1 ; 3 \right], \forall x$.
Ta có: $\dfrac{1}{2{{\sin }^{2}}x}=\dfrac{1}{1-\cos 2x}=\dfrac{2}{2-2\cos 2x}=\dfrac{2}{\left( -2\cos 2x+1 \right)+1}=\dfrac{2}{t+1}$.
Phương trình trở thành: $f\left( t \right)=\dfrac{2}{t+1} \left( * \right)$, (với $t\ne -1$ ). Kết hợp với $t\in \left[ -1;3 \right]$ ta xét nghiệm của phương trình $\left( * \right)$ trên nửa khoảng $\left( -1;3 \right]$.
Đồ thị hàm số $y=\dfrac{2}{x+1}$ có tiệm cận ngang $y=0$, tiệm cần đứng $x=-1$ và đi qua các điểm đặc biệt $\left( 0 ; 2 \right), \left( 1 ; 1 \right) , \left( 3 ; \dfrac{1}{2} \right)$. Xét sự tương giao trên cùng một hệ trục tọa độ:
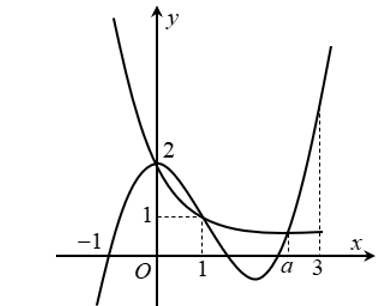Dựa vào đồ thị, trên $\left( -1;3 \right]$ thì đồ thị hàm số $y=\dfrac{2}{x+1}$ cắt đồ thị hàm số $y=f\left( x \right)$ tại ba điểm phân biệt có hoành độ $x=0 , x=1 , x=a\in \left( 1 ; 3 \right)$.
Bảng biến thiên của hàm số: $t=-2\cos 2x+1$ trên đoạn $\left[ -\pi ;3\pi \right]$
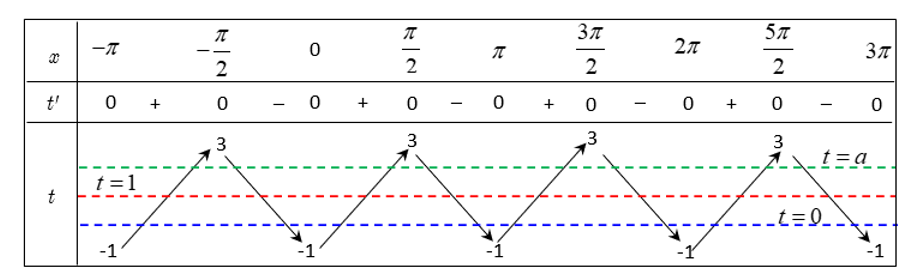
Dựa vào bảng biến thiên:
Với $t=0$, phương trình có $8$ nghiệm phân biệt.
Với $t=1$, phương trình có $8$ nghiệm phân biệt.
Với $t=a\in \left( 1 ; 3 \right)$, phương trình có $8$ nghiệm phân biệt.
Vậy phương trình đã cho có tất cả $24$ nghiệm thuộc đoạn $\left[ -\pi ;3\pi \right]$.
Ta có: $\dfrac{1}{2{{\sin }^{2}}x}=\dfrac{1}{1-\cos 2x}=\dfrac{2}{2-2\cos 2x}=\dfrac{2}{\left( -2\cos 2x+1 \right)+1}=\dfrac{2}{t+1}$.
Phương trình trở thành: $f\left( t \right)=\dfrac{2}{t+1} \left( * \right)$, (với $t\ne -1$ ). Kết hợp với $t\in \left[ -1;3 \right]$ ta xét nghiệm của phương trình $\left( * \right)$ trên nửa khoảng $\left( -1;3 \right]$.
Đồ thị hàm số $y=\dfrac{2}{x+1}$ có tiệm cận ngang $y=0$, tiệm cần đứng $x=-1$ và đi qua các điểm đặc biệt $\left( 0 ; 2 \right), \left( 1 ; 1 \right) , \left( 3 ; \dfrac{1}{2} \right)$. Xét sự tương giao trên cùng một hệ trục tọa độ:
Bảng biến thiên của hàm số: $t=-2\cos 2x+1$ trên đoạn $\left[ -\pi ;3\pi \right]$
Dựa vào bảng biến thiên:
Với $t=0$, phương trình có $8$ nghiệm phân biệt.
Với $t=1$, phương trình có $8$ nghiệm phân biệt.
Với $t=a\in \left( 1 ; 3 \right)$, phương trình có $8$ nghiệm phân biệt.
Vậy phương trình đã cho có tất cả $24$ nghiệm thuộc đoạn $\left[ -\pi ;3\pi \right]$.
Đáp án A.