Google
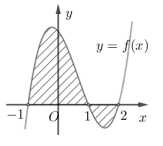
Câu hỏi: Cho hàm số $f\left( x \right)$ liên tục trê $\mathbb{R}$. Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y=f\left( x \right),y=0,x=-1,x=2$ (như hình vẽ bên).
Mệnh đề nào dưới đây đúng?
A. $S=\int\limits_{-1}^{1}{f\left( x \right)dx}+\int\limits_{1}^{2}{f\left( x \right)dx}$.
B. $S=\int\limits_{-1}^{1}{f\left( x \right)dx}-\int\limits_{1}^{2}{f\left( x \right)dx}$.
C. $S=-\int\limits_{-1}^{1}{f\left( x \right)dx}-\int\limits_{1}^{2}{f\left( x \right)dx}$.
D. $S=-\int\limits_{-1}^{1}{f\left( x \right)dx}+\int\limits_{1}^{2}{f\left( x \right)dx}$.
A. $S=\int\limits_{-1}^{1}{f\left( x \right)dx}+\int\limits_{1}^{2}{f\left( x \right)dx}$.
B. $S=\int\limits_{-1}^{1}{f\left( x \right)dx}-\int\limits_{1}^{2}{f\left( x \right)dx}$.
C. $S=-\int\limits_{-1}^{1}{f\left( x \right)dx}-\int\limits_{1}^{2}{f\left( x \right)dx}$.
D. $S=-\int\limits_{-1}^{1}{f\left( x \right)dx}+\int\limits_{1}^{2}{f\left( x \right)dx}$.
Ta có $S=\int\limits_{-1}^{1}{f\left( x \right)dx}-\int\limits_{1}^{2}{f\left( x \right)dx}$.
Đáp án B.