Google
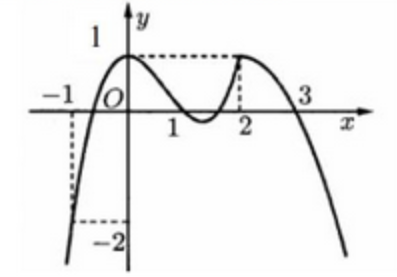
Câu hỏi: Cho hàm số $f\left( x \right)$ có đồ thị ${f}'\left( x \right)$ như hình vẽ
Hàm số $g\left( x \right)=f\left( {{x}^{2}} \right)-\dfrac{{{x}^{6}}}{3}+{{x}^{4}}-{{x}^{2}}$ đồng biến trên khoảng nào dưới đây?
A. $\left( -1;0 \right)$.
B. $\left( -\dfrac{1}{2};\dfrac{1}{2} \right)$.
C. $\left( \dfrac{3}{2};2 \right)$.
D. $\left( 0;1 \right)$.
A. $\left( -1;0 \right)$.
B. $\left( -\dfrac{1}{2};\dfrac{1}{2} \right)$.
C. $\left( \dfrac{3}{2};2 \right)$.
D. $\left( 0;1 \right)$.
Ta có
${g}'\left( x \right)=2x{f}'\left( {{x}^{2}} \right)-\left( 2{{x}^{5}}-4{{x}^{3}}+2x \right)$
$=2x\left( {f}'\left( {{x}^{2}} \right)-\left( {{x}^{4}}-2{{x}^{2}}+1 \right) \right)$
Xét phương trình ${f}'\left( {{x}^{2}} \right)-\left( {{x}^{4}}-2{{x}^{2}}+1 \right)=0$
Đặt $t={{x}^{2}}$ ta được phương trình ${f}'\left( t \right)={{t}^{2}}-2t+1$
Suy ra phương trình có 3 nghiệm $t=0;t=1;t=2.$
Hay phương trình ${f}'\left( {{x}^{2}} \right)-\left( {{x}^{4}}-2{{x}^{2}}+1 \right)=0$ có 5 nghiệm $x=0;x=\pm 1;x=\pm \sqrt{2}$
Ta có bảng xét dấu của ${g}'\left( x \right)$
Suy ra hàm số đồng biến trên $\left( 0;1 \right)$
${g}'\left( x \right)=2x{f}'\left( {{x}^{2}} \right)-\left( 2{{x}^{5}}-4{{x}^{3}}+2x \right)$
$=2x\left( {f}'\left( {{x}^{2}} \right)-\left( {{x}^{4}}-2{{x}^{2}}+1 \right) \right)$
Xét phương trình ${f}'\left( {{x}^{2}} \right)-\left( {{x}^{4}}-2{{x}^{2}}+1 \right)=0$
Đặt $t={{x}^{2}}$ ta được phương trình ${f}'\left( t \right)={{t}^{2}}-2t+1$
Hay phương trình ${f}'\left( {{x}^{2}} \right)-\left( {{x}^{4}}-2{{x}^{2}}+1 \right)=0$ có 5 nghiệm $x=0;x=\pm 1;x=\pm \sqrt{2}$
Ta có bảng xét dấu của ${g}'\left( x \right)$
Suy ra hàm số đồng biến trên $\left( 0;1 \right)$
Đáp án D.