Google
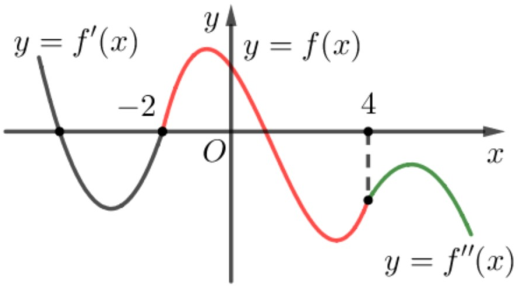
Câu hỏi: Cho hàm số $f\left( x \right)$ có đạo hàm cấp hai liên tục trên $R$. Hình vẽ bên dưới là đồ thị của hàm số $y={f}'\left( x \right)$ trên $\left( -\infty ;-2 \right]$, đồ thị hàm số $y=f\left( x \right)$ trên $\left[ -2;4 \right]$,đồ thị $y=f''\left( x \right)$ trên $\left[ 4;+\infty \right)$.
Hàm số $y=f\left( x \right)$ có bao nhiêu điểm cực tiểu.
A. $2$
B. $3$
C. $1$
D. $4$
A. $2$
B. $3$
C. $1$
D. $4$
Trên $\left( -\infty ;-2 \right)$ hàm số $y=f\left( x \right)$ có một điểm cực tiểu.
Trên $\left( 2;4 \right)$ hàm số $y=f\left( x \right)$ có một điểm cực tiểu.
Trên $\left( 4;+\infty \right)$ vì $f''\left( x \right)<0$ nên $y=f'\left( x \right)$ nghịch biến, mà $f'\left( 4 \right)>0$ nên hàm số $y=f\left( x \right)$ có một cực tiểu.
Vậy hàm số $y=f\left( x \right)$ có 3 cực tiểu.
Trên $\left( 2;4 \right)$ hàm số $y=f\left( x \right)$ có một điểm cực tiểu.
Trên $\left( 4;+\infty \right)$ vì $f''\left( x \right)<0$ nên $y=f'\left( x \right)$ nghịch biến, mà $f'\left( 4 \right)>0$ nên hàm số $y=f\left( x \right)$ có một cực tiểu.
Vậy hàm số $y=f\left( x \right)$ có 3 cực tiểu.
Đáp án B.