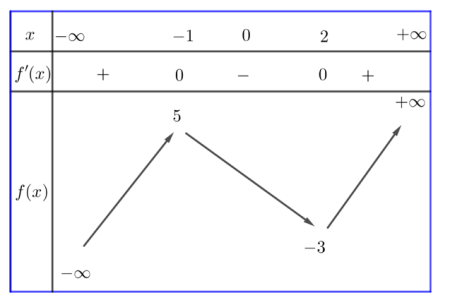
Cho hàm số $f\left( x \right)$ có bảng biến thiên như sau: Số...

$\int{\dfrac{1}{x}dx}=\ln x+C$
${f}'\left[ f\left( x \right)+2 \right]=0\Leftrightarrow \left[ \begin{aligned}
& f\left( x \right)+2=-1 \\
& f\left( x \right)+2=2 \\
\end{aligned} \right.$$\Leftrightarrow \left[ \begin{aligned}
& f\left( x \right)=-3 \\
& f\left( x \right)=0 \\
\end{aligned} \right.$
* $f\left( x \right)=-3\Leftrightarrow \left[ \begin{aligned}
& x=2 \\
& x=a \left( a<-1 \right) \\
\end{aligned} \right.$
$f\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=b\left( b<-1 \right) \\
& x=c\left( -1<c<2 \right) \\
& x=d\left( d>2 \right) \\
\end{aligned} \right.$
Vậy phương trình đã cho có $5$ nghiệm thực phân biệt