Google
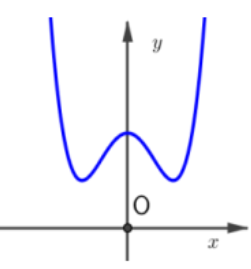
Câu hỏi: Cho hàm số $f\left( x \right)$, biết hàm số ${{f}'}'\left( x \right)$ là hàm đa thức bậc bốn có đồ thị như hình vẽ bên. Đặt $g\left( x \right)=2f\left( \dfrac{1}{2}{{x}^{2}} \right)+f\left( -{{x}^{2}}+6 \right)$ với $g\left( 0 \right)>0$ và $g\left( 2 \right)<0$. Số điểm cực tiểu của hàm số $y=\left| g\left( x \right) \right|$ là
A. 3.
B. 4.
C. 5.
D. 7.
B. 4.
C. 5.
D. 7.
Xét $g\left( x \right)=2f\left( \dfrac{1}{2}{{x}^{2}} \right)+f\left( -{{x}^{2}}+6 \right)$
Có ${g}'\left( x \right)=2x.{f}'\left( \dfrac{1}{2}{{x}^{2}} \right)-2x.{f}'\left( -{{x}^{2}}+6 \right)$
Xét ${g}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& 2x=0 \\
& {f}'\left( \dfrac{1}{2}{{x}^{2}} \right)={f}'\left( -{{x}^{2}}+6 \right) \left( * \right) \\
\end{aligned} \right.$
Theo đồ thị hàm số vì ${{f}'}'\left( x \right)>0$ với $\forall x\in \mathbb{R}$ do đó ${f}'\left( x \right)$ đồng biến trên $\mathbb{R}$
Từ phương trình $\left( * \right)$ suy ra $\dfrac{1}{2}{{x}^{2}}=-{{x}^{2}}+6\Leftrightarrow x=\pm 2$
Vậy phương trình ${g}'\left( x \right)=0$ có ba nghiệm phân biệt đan dấu $\left[ \begin{aligned}
& x=0 \\
& x=\pm 2 \\
\end{aligned} \right.$
Ta có bảng biến thiên
Do $g\left( x \right)$ là hàm số chẵn nên $g\left( -2 \right)=g\left( 2 \right)<0$
Vậy số điểm cực tiểu của hàm số $y=\left| g\left( x \right) \right|$ là 4.
Có ${g}'\left( x \right)=2x.{f}'\left( \dfrac{1}{2}{{x}^{2}} \right)-2x.{f}'\left( -{{x}^{2}}+6 \right)$
Xét ${g}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& 2x=0 \\
& {f}'\left( \dfrac{1}{2}{{x}^{2}} \right)={f}'\left( -{{x}^{2}}+6 \right) \left( * \right) \\
\end{aligned} \right.$
Theo đồ thị hàm số vì ${{f}'}'\left( x \right)>0$ với $\forall x\in \mathbb{R}$ do đó ${f}'\left( x \right)$ đồng biến trên $\mathbb{R}$
Từ phương trình $\left( * \right)$ suy ra $\dfrac{1}{2}{{x}^{2}}=-{{x}^{2}}+6\Leftrightarrow x=\pm 2$
Vậy phương trình ${g}'\left( x \right)=0$ có ba nghiệm phân biệt đan dấu $\left[ \begin{aligned}
& x=0 \\
& x=\pm 2 \\
\end{aligned} \right.$
Ta có bảng biến thiên
Vậy số điểm cực tiểu của hàm số $y=\left| g\left( x \right) \right|$ là 4.
Đáp án B.