Google
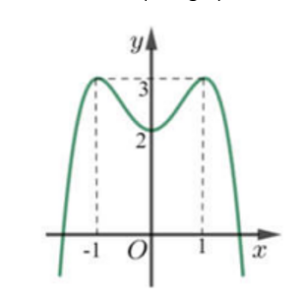
Câu hỏi: Cho hàm số $f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c$ có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình $f\left( x \right)=\dfrac{2022}{1010}$ là
A. $2$.
B. $3$.
C. $0$.
D. $4$.
A. $2$.
B. $3$.
C. $0$.
D. $4$.
Số nghiệm của phương trình $f\left( x \right)=\dfrac{2022}{1010}$ là số giao điểm của đồ thị hàm số $y=f\left( x \right)$ và đường thẳng $y=\dfrac{2022}{1010}$ (đường thẳng song song với trục $Ox$ và cắt trục $Oy$ tại điểm có tung độ bằng $\dfrac{2022}{1010}$ ). Dựa vào đồ thị ta thấy phương trình có 4 nghiệm.
Đáp án D.