Câu hỏi: Cho hàm số đa thức bậc ba ${y=f(x)}$ có đồ thị như hình vẽ.
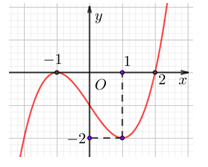
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số ${y=\dfrac{(x+1)({{x}^{2}}-1)}{f(x)}}$ là
A. ${1}$.
B. ${2}$.
C. ${3}$.
D. ${4}$.

Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số ${y=\dfrac{(x+1)({{x}^{2}}-1)}{f(x)}}$ là
A. ${1}$.
B. ${2}$.
C. ${3}$.
D. ${4}$.
Tập xác định : $D=\mathbb{R}\backslash \left\{ -1;2 \right\}.$
Từ đồ thị ta có $f(x)=a{{(x+1)}^{2}}\left( x-2 \right), (a>0).$
$\Rightarrow y=\dfrac{\left( x+1 \right)\left( {{x}^{2}}-1 \right)}{a{{\left( x+1 \right)}^{2}}\left( x-2 \right)}=\dfrac{x+1}{a\left( x-2 \right)},\left( x\ne -1 \right)$
Ta có ${{\lim }_{x\to \pm \infty }}f\left( x \right)=\dfrac{1}{a}\Rightarrow TCN:y=\dfrac{1}{a}$
Lại có $\left\{ \begin{aligned}
& \underset{x\to {{2}^{+}}}{\mathop{\lim }} f\left( x \right)=+\infty \\
& \underset{x\to {{2}^{-}}}{\mathop{\lim }} f\left( x \right)=-\infty \\
\end{aligned} \right.\Rightarrow $ TCĐ : $ x=2$.
Vậy đồ thị hàm số đã cho có hai đường tiệm cận.
Từ đồ thị ta có $f(x)=a{{(x+1)}^{2}}\left( x-2 \right), (a>0).$
$\Rightarrow y=\dfrac{\left( x+1 \right)\left( {{x}^{2}}-1 \right)}{a{{\left( x+1 \right)}^{2}}\left( x-2 \right)}=\dfrac{x+1}{a\left( x-2 \right)},\left( x\ne -1 \right)$
Ta có ${{\lim }_{x\to \pm \infty }}f\left( x \right)=\dfrac{1}{a}\Rightarrow TCN:y=\dfrac{1}{a}$
Lại có $\left\{ \begin{aligned}
& \underset{x\to {{2}^{+}}}{\mathop{\lim }} f\left( x \right)=+\infty \\
& \underset{x\to {{2}^{-}}}{\mathop{\lim }} f\left( x \right)=-\infty \\
\end{aligned} \right.\Rightarrow $ TCĐ : $ x=2$.
Vậy đồ thị hàm số đã cho có hai đường tiệm cận.
Đáp án B.