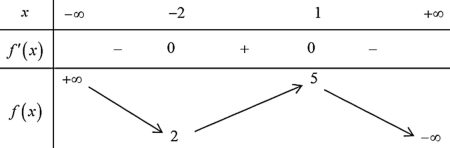
: Cho hàm số có bảng biến thiên như sau: Số điểm cực đại của hàm số $g\left( x \right)={{\left[ f\left( 2{{x}^{2}}+x \right) \right]}^{2}}$ là

Phương pháp:
- Sử dụng công thức tính đạo hàm hàm hợp tính $g'\left( x \right).$
- Sử dụng tương giao giải phương trình $g'\left( x \right)=0.$
- Lập bảng xét dấu $g'\left( x \right).$
Cách giải:
Ta có $g\left( x \right)={{\left[ f\left( 2{{x}^{2}}+x \right) \right]}^{2}}$
$\Rightarrow g'\left( x \right)=2\left( 4x+1 \right).f'\left( 2{{x}^{2}}+x \right)f\left( 2{{x}^{2}}+x \right)$
$g'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& 4x+1=0\Leftrightarrow x=-\dfrac{1}{4} \\
& f'\left( 2{{x}^{2}}+x \right)=0\left( 1 \right) \\
& f\left( 2{{x}^{2}}+x \right)=0\text{ }\left( 2 \right) \\
\end{aligned} \right.$
Dựa vào BBT ta thấy:
$f'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=-2 \\
& x=1 \\
\end{aligned} \right., $ do đó $ \left( 1 \right)\Leftrightarrow \left[ \begin{aligned}
& 2{{x}^{2}}+x=-2\left( vonghiem \right) \\
& 2{{x}^{2}}+x=1 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& x=\dfrac{1}{2} \\
& x=-1 \\
\end{aligned} \right..$
$f\left( x \right)=0$ có 1 nghiệm $x=a>1,$ do đó $\left( 2 \right)\Leftrightarrow 2{{x}^{2}}+x=a\left( a>1 \right).$
Xét hàm số $f\left( x \right)=2{{x}^{2}}+x$ ta có $f'\left( x \right)=4x+1=0\Leftrightarrow x=-\dfrac{1}{4}.$
Bảng biến thiên:

Dựa vào BBT ta thấy phương trình $f\left( x \right)=a$ có 2 nghiệm phân biệt $x=b,x=c$ và $b<-1,c>\dfrac{1}{2}.$
Khi đó ta có bảng xét dấu $y=g'\left( x \right)$ như sau:

Dựa vào bảng biến thiên ta thấy hàm số $y=g\left( x \right)$ có 3 điểm cực đại.