Google
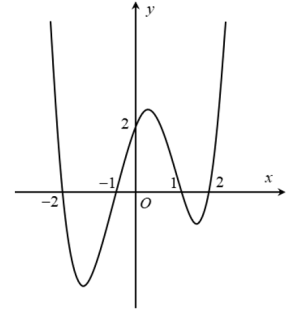
Câu hỏi: Cho hàm số bậc năm $y=f\left( x \right)$ có đồ thị ${f}'(x) $ là đường cong trong hình vẽ sau.
Số điểm cực trị của hàm số $y=f\left( {{x}^{3}}-3{{x}^{2}} \right)-\dfrac{3}{4}{{x}^{4}}+2{{x}^{3}}+2023$ là:
A. $8$.
B. $7$.
C. $6$.
D. $10$
A. $8$.
B. $7$.
C. $6$.
D. $10$
Ta có ${y}'=\left( 3{{x}^{2}}-6x \right){f}'\left( {{x}^{3}}-3{{x}^{2}} \right)-3{{x}^{3}}+6{{x}^{2}}=\left( 3{{x}^{2}}-6x \right)\left[ {f}'\left( {{x}^{3}}-3{{x}^{2}} \right)-x \right]$
Xét hàm số $h\left( x \right)={f}'\left( {{x}^{3}}-3{{x}^{2}} \right)$
Ta có ${h}'\left( x \right)=\left( 3{{x}^{2}}-6x \right){f}''\left( {{x}^{3}}-3{{x}^{2}} \right)=0\Leftrightarrow \left[ \begin{matrix}
3{{x}^{2}}-6x=0 \\
\begin{matrix}
{{x}^{3}}-3{{x}^{2}}=a & \left( -2<a<-1 \right) \\
{{x}^{3}}-3{{x}^{2}}=b & \left( 0<b<1 \right) \\
{{x}^{3}}-3{{x}^{2}}=c & \left( 1<c<2 \right) \\
\end{matrix} \\
\end{matrix} \right.$
Xét hàm số $g\left( x \right)={{x}^{3}}-3{{x}^{2}}$.
Ta có ${g}'\left( x \right)=3{{x}^{2}}-6x=0\Leftrightarrow \left[ \begin{matrix}
x=0 \\
x=2 \\
\end{matrix} \right.$
Từ bảng biến thiên ta thấy được:
$\left[ \begin{matrix}
3{{x}^{2}}-6x=0 \\
\begin{matrix}
{{x}^{3}}-3{{x}^{2}}=a & \left( -2<a<-1 \right) \\
{{x}^{3}}-3{{x}^{2}}=b & \left( 0<b<1 \right) \\
{{x}^{3}}-3{{x}^{2}}=c & \left( 1<c<2 \right) \\
\end{matrix} \\
\end{matrix} \right.\Leftrightarrow \left[ \begin{matrix}
x=0 & {} \\
x=2 & {} \\
x={{a}_{1}} & \left( {{a}_{1}}<0 \right) \\
x={{a}_{2}} & \left( 0<{{a}_{2}}<2 \right) \\
x={{a}_{3}} & \left( 2<{{a}_{3}} \right) \\
x={{b}_{1}} & \left( {{a}_{3}}<{{b}_{1}} \right) \\
x={{c}_{1}} & \left( {{b}_{1}}<{{c}_{1}} \right) \\
\end{matrix} \right.$
Khi đó ta có được bảng biến thiên của $h\left( x \right)={f}'\left( {{x}^{3}}-3{{x}^{2}} \right)$ :
Xét hàm số $h\left( x \right)={f}'\left( {{x}^{3}}-3{{x}^{2}} \right)$
Ta có ${h}'\left( x \right)=\left( 3{{x}^{2}}-6x \right){f}''\left( {{x}^{3}}-3{{x}^{2}} \right)=0\Leftrightarrow \left[ \begin{matrix}
3{{x}^{2}}-6x=0 \\
\begin{matrix}
{{x}^{3}}-3{{x}^{2}}=a & \left( -2<a<-1 \right) \\
{{x}^{3}}-3{{x}^{2}}=b & \left( 0<b<1 \right) \\
{{x}^{3}}-3{{x}^{2}}=c & \left( 1<c<2 \right) \\
\end{matrix} \\
\end{matrix} \right.$
Xét hàm số $g\left( x \right)={{x}^{3}}-3{{x}^{2}}$.
Ta có ${g}'\left( x \right)=3{{x}^{2}}-6x=0\Leftrightarrow \left[ \begin{matrix}
x=0 \\
x=2 \\
\end{matrix} \right.$
$\left[ \begin{matrix}
3{{x}^{2}}-6x=0 \\
\begin{matrix}
{{x}^{3}}-3{{x}^{2}}=a & \left( -2<a<-1 \right) \\
{{x}^{3}}-3{{x}^{2}}=b & \left( 0<b<1 \right) \\
{{x}^{3}}-3{{x}^{2}}=c & \left( 1<c<2 \right) \\
\end{matrix} \\
\end{matrix} \right.\Leftrightarrow \left[ \begin{matrix}
x=0 & {} \\
x=2 & {} \\
x={{a}_{1}} & \left( {{a}_{1}}<0 \right) \\
x={{a}_{2}} & \left( 0<{{a}_{2}}<2 \right) \\
x={{a}_{3}} & \left( 2<{{a}_{3}} \right) \\
x={{b}_{1}} & \left( {{a}_{3}}<{{b}_{1}} \right) \\
x={{c}_{1}} & \left( {{b}_{1}}<{{c}_{1}} \right) \\
\end{matrix} \right.$
Khi đó ta có được bảng biến thiên của $h\left( x \right)={f}'\left( {{x}^{3}}-3{{x}^{2}} \right)$ :
Khi đó phương trình ${f}'\left( {{x}^{3}}-3{{x}^{2}} \right)-x=0\Leftrightarrow {f}'\left( {{x}^{3}}-3{{x}^{2}} \right)=x$ có $5$ nghiệm phân biệt khác $0$ và $2$ nên phương trình ${y}'=\left( 3{{x}^{2}}-6x \right)\left[ {f}'\left( {{x}^{3}}-3{{x}^{2}} \right)-x \right]$ có $7$ nghiệm phân biệt.
Vậy hàm số $y=f\left( {{x}^{3}}-3{{x}^{2}} \right)-\dfrac{3}{4}{{x}^{4}}+2{{x}^{3}}+2023$ có $7$ điểm cực trị.
Vậy hàm số $y=f\left( {{x}^{3}}-3{{x}^{2}} \right)-\dfrac{3}{4}{{x}^{4}}+2{{x}^{3}}+2023$ có $7$ điểm cực trị.
Đáp án B.