Google
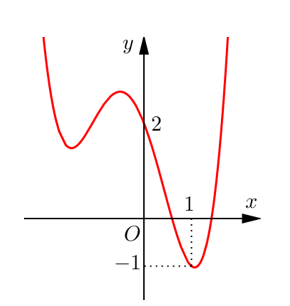
Câu hỏi: Cho hàm số bậc năm $f\left( x \right).$ Hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ
Số điểm cực trị của hàm số $g\left( x \right)=f\left( x \right)+\dfrac{2}{3}{{x}^{3}}-2{{x}^{2}}+3x$ là
A. $0$.
B. $1$.
C. $3$.
D. $2$.
A. $0$.
B. $1$.
C. $3$.
D. $2$.
Ta có ${g}'\left( x \right)={f}'\left( x \right)+2{{x}^{2}}-4x+3$
Khi đó ${g}'\left( x \right)=0\Leftrightarrow {f}'\left( x \right)=-2{{x}^{2}}+4x-3 \left( 1 \right)$.
Ta thấy số nghiệm của $\left( 1 \right)$ là số giao điểm của $y={f}'\left( x \right)$ và parabol $y=-2{{x}^{2}}+4x-3$ (hình vẽ).
Từ đồ thị ta thấy $\left( 1 \right)$ có nghiệm bội chẵn. Vậy hàm số $g\left( x \right)=f\left( x \right)+\dfrac{2}{3}{{x}^{3}}-2{{x}^{2}}+3x$ không có cực trị.
Khi đó ${g}'\left( x \right)=0\Leftrightarrow {f}'\left( x \right)=-2{{x}^{2}}+4x-3 \left( 1 \right)$.
Ta thấy số nghiệm của $\left( 1 \right)$ là số giao điểm của $y={f}'\left( x \right)$ và parabol $y=-2{{x}^{2}}+4x-3$ (hình vẽ).
Đáp án A.