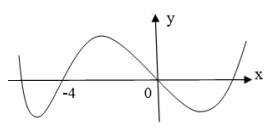
Cho hàm số bậc bốn $y=f(x)$ có đồ thị như hình vẽ. Số điểm cực trị...

Ta có $g(x)=f({{x}^{3}}-3{{x}^{2}})\Rightarrow g'(x)=(3{{x}^{2}}-6x).f'({{x}^{3}}-3{{x}^{2}})$.
$g'(x)=0\Leftrightarrow \left[ \begin{matrix}
3{{x}^{2}}-6x=0 \\
f'({{x}^{3}}-3{{x}^{2}})=0 \\
\end{matrix} \right.\Leftrightarrow \left[ \begin{matrix}
x=0 \\
x=2 \\
{{x}^{3}}-3{{x}^{2}}=a (a<-4) \\
{{x}^{3}}-3{{x}^{2}}=b (-4<b<0) \\
{{x}^{3}}-3{{x}^{2}}=c (c>0) \\
\end{matrix} \right.$
Ta có bảng biến thiên của hàm số $y={{x}^{3}}-3{{x}^{2}}$.
Dựa vào bảng biến thiên ta có: ${{x}^{3}}-3{{x}^{2}}=a (a<-4)$ có 1 nghiệm.
${{x}^{3}}-3{{x}^{2}}=b (-4<b<0)$ có 3 nghiệm.
${{x}^{3}}-3{{x}^{2}}=c (c>0)$ có 1 nghiệm.
Vậy số điểm cực trị của hàm số $g(x)=f({{x}^{3}}-3{{x}^{2}})$ là 7.