Google
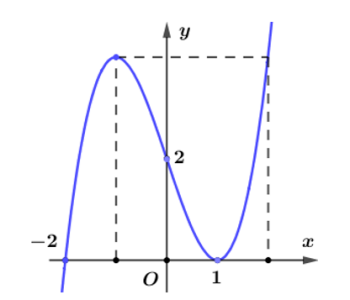
Câu hỏi: Cho hàm số bậc bốn $y=f\left( x \right)$. Hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ.
Số điểm cực trị của hàm số $g\left( x \right)=f\left( x \right)+\dfrac{1}{3}{{x}^{3}}+\dfrac{1}{2}{{x}^{2}}-2x-3$ là
A. $1$.
B. $2$.
C. $3$.
D. $0$.
A. $1$.
B. $2$.
C. $3$.
D. $0$.
Đạo hàm ${g}'\left( x \right)={f}'\left( x \right)+{{x}^{2}}+x-2$.
${g}'\left( x \right)=0\Leftrightarrow {f}'\left( x \right)=-{{x}^{2}}-x+2$.
Vẽ đồ thị hàm số $y=-{{x}^{2}}-x+2$
Suy ra ${g}'\left( x \right)=0$ có $3$ nghiệm và đổi dấu qua các nghiệm đó.
Vậy $g\left( x \right)$ có ba điểm cực trị.
${g}'\left( x \right)=0\Leftrightarrow {f}'\left( x \right)=-{{x}^{2}}-x+2$.
Vẽ đồ thị hàm số $y=-{{x}^{2}}-x+2$
Vậy $g\left( x \right)$ có ba điểm cực trị.
Đáp án C.