Google
Câu hỏi: Cho hàm số bậc bốn $y=f\left( x \right)$ có đồ thị như hình vẽ
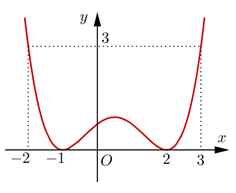
Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{{{\left( {{x}^{2}}-4 \right)}^{2}}\left( x-3 \right)\left( {{x}^{3}}+1 \right)}{f\left( f\left( x \right)-1 \right)}$ là
A. 2.
B. 5.
C. 3.
D. 4.
Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{{{\left( {{x}^{2}}-4 \right)}^{2}}\left( x-3 \right)\left( {{x}^{3}}+1 \right)}{f\left( f\left( x \right)-1 \right)}$ là
A. 2.
B. 5.
C. 3.
D. 4.
Từ đồ thị hàm số ta có $f\left( x \right)=a{{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{2}},a>0$, do $f\left( 3 \right)=f\left( -2 \right)=3\Rightarrow a=\dfrac{3}{16}$.
Vậy $f\left( x \right)=\dfrac{3}{16}{{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{2}}\Rightarrow f\left( x \right)-1=\dfrac{3}{16}{{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{2}}-1$.
Khi đó $f\left( f\left( x \right)-1 \right)=\dfrac{3}{16}.{{\left[ \dfrac{3}{16}{{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{2}} \right]}^{2}}{{\left[ \dfrac{3}{16}{{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{2}}-3 \right]}^{2}}$
$=\dfrac{{{3}^{5}}}{{{16}^{5}}}{{\left( x+1 \right)}^{4}}{{\left( x-2 \right)}^{4}}{{\left[ {{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{2}}-16 \right]}^{2}}$
$=\dfrac{{{3}^{5}}}{{{16}^{5}}}{{\left( x+1 \right)}^{4}}{{\left( x-2 \right)}^{4}}{{\left( x-3 \right)}^{2}}{{\left( x+2 \right)}^{2}}{{\left( {{x}^{2}}-x+2 \right)}^{2}}$
Vậy $y=\dfrac{{{\left( {{x}^{2}}-4 \right)}^{2}}\left( x-3 \right)\left( {{x}^{3}}+1 \right)}{f\left( f\left( x \right)-1 \right)}=\dfrac{{{\left( x-2 \right)}^{2}}{{\left( x+2 \right)}^{2}}\left( x-3 \right)\left( x+1 \right)\left( {{x}^{2}}-x+1 \right)}{\dfrac{{{3}^{5}}}{{{16}^{5}}}{{\left( x+1 \right)}^{4}}{{\left( x-2 \right)}^{4}}{{\left( x-3 \right)}^{2}}{{\left( x+2 \right)}^{2}}{{\left( {{x}^{2}}-x+2 \right)}^{2}}}$
Khi đó $\underset{x\to {{\left( -1 \right)}^{+}}}{\mathop{\lim y}} =+\infty ,\underset{x\to {{3}^{+}}}{\mathop{\lim y}} =+\infty ,\underset{x\to {{2}^{+}}}{\mathop{\lim y}} =-\infty ,\underset{x\to \left( -2 \right)}{\mathop{\lim y}} =a,a>0$ (a hữu hạn)
Ta có đồ thị hàm số có các đường tiệm cận đứng là: $x=-1,x=3,x=2$.
Do $\underset{x\to +\infty }{\mathop{\lim y}} =0;\underset{x\to -\infty }{\mathop{\lim y}} =0$. Vậy đồ thị hàm số có tiệm cận ngang $y=0$.
Vậy đồ thị hàm số có 4 đường tiệm cận.
Vậy $f\left( x \right)=\dfrac{3}{16}{{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{2}}\Rightarrow f\left( x \right)-1=\dfrac{3}{16}{{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{2}}-1$.
Khi đó $f\left( f\left( x \right)-1 \right)=\dfrac{3}{16}.{{\left[ \dfrac{3}{16}{{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{2}} \right]}^{2}}{{\left[ \dfrac{3}{16}{{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{2}}-3 \right]}^{2}}$
$=\dfrac{{{3}^{5}}}{{{16}^{5}}}{{\left( x+1 \right)}^{4}}{{\left( x-2 \right)}^{4}}{{\left[ {{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{2}}-16 \right]}^{2}}$
$=\dfrac{{{3}^{5}}}{{{16}^{5}}}{{\left( x+1 \right)}^{4}}{{\left( x-2 \right)}^{4}}{{\left( x-3 \right)}^{2}}{{\left( x+2 \right)}^{2}}{{\left( {{x}^{2}}-x+2 \right)}^{2}}$
Vậy $y=\dfrac{{{\left( {{x}^{2}}-4 \right)}^{2}}\left( x-3 \right)\left( {{x}^{3}}+1 \right)}{f\left( f\left( x \right)-1 \right)}=\dfrac{{{\left( x-2 \right)}^{2}}{{\left( x+2 \right)}^{2}}\left( x-3 \right)\left( x+1 \right)\left( {{x}^{2}}-x+1 \right)}{\dfrac{{{3}^{5}}}{{{16}^{5}}}{{\left( x+1 \right)}^{4}}{{\left( x-2 \right)}^{4}}{{\left( x-3 \right)}^{2}}{{\left( x+2 \right)}^{2}}{{\left( {{x}^{2}}-x+2 \right)}^{2}}}$
Khi đó $\underset{x\to {{\left( -1 \right)}^{+}}}{\mathop{\lim y}} =+\infty ,\underset{x\to {{3}^{+}}}{\mathop{\lim y}} =+\infty ,\underset{x\to {{2}^{+}}}{\mathop{\lim y}} =-\infty ,\underset{x\to \left( -2 \right)}{\mathop{\lim y}} =a,a>0$ (a hữu hạn)
Ta có đồ thị hàm số có các đường tiệm cận đứng là: $x=-1,x=3,x=2$.
Do $\underset{x\to +\infty }{\mathop{\lim y}} =0;\underset{x\to -\infty }{\mathop{\lim y}} =0$. Vậy đồ thị hàm số có tiệm cận ngang $y=0$.
Vậy đồ thị hàm số có 4 đường tiệm cận.
Đáp án D.