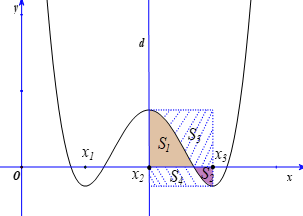
Câu hỏi: Cho hàm số bậc bốn $y=f\left( x \right)$ có đồ thị $\left( C \right)$ như hình vẽ bên. Biết hàm số $y=f\left( x \right)$ đạt cực trị tại các điểm ${{x}_{1}},{{x}_{2}},{{x}_{3}}$ thỏa mãn ${{x}_{3}}={{x}_{1}}+2$, $f\left( {{x}_{1}} \right)+f\left( {{x}_{3}} \right)+\dfrac{2}{3}f\left( {{x}_{2}} \right)=0$ và $\left( C \right)$ nhận đường thẳng $d:x={{x}_{2}}$ làm trục đối xứng. Gọi ${{S}_{1}},{{S}_{2}},{{S}_{3}},{{S}_{4}}$ là diện tích của các miền hình phẳng được đánh dấu như hình bên. Tỉ số $\dfrac{{{S}_{1}}+{{S}_{2}}}{{{S}_{3}}+{{S}_{4}}}$ gần kết quả nào nhất?
A. $0,60$.
B. $0,55$.
C. $0,65$.
D. $0,70$.
Lại có $f\left( {{x}_{1}} \right)+f\left( {{x}_{3}} \right)+\dfrac{2}{3}f\left( {{x}_{2}} \right)=0\Rightarrow -2k+2c+\dfrac{2}{3}c=0\Leftrightarrow c=\dfrac{3}{4}k$
Suy ra: $y=g\left( x \right)=k\left( {{x}^{4}}-2{{x}^{2}} \right)+\dfrac{3}{4}k$
Khi đó: ${{S}_{1}}+{{S}_{2}}=k\int\limits_{0}^{1}{\left| {{x}^{4}}-2{{x}^{2}}+\dfrac{3}{4} \right|}\text{d}x=\dfrac{28\sqrt{2}-17}{60}k$.
Ta lại có: $g\left( 0 \right)-g\left( 1 \right)=k$ $\Rightarrow {{S}_{1}}+{{S}_{2}}+{{S}_{3}}+{{S}_{4}}=k.1=k$.
Suy ra ${{S}_{3}}+{{S}_{4}}=k-\dfrac{28\sqrt{2}-17}{60}k=\dfrac{77-28\sqrt{2}}{60}k\Rightarrow \dfrac{{{S}_{1}}+{{S}_{2}}}{{{S}_{3}}+{{S}_{4}}}=\dfrac{28\sqrt{2}-17}{77-28\sqrt{2}}\approx 0,604$
A. $0,60$.
B. $0,55$.
C. $0,65$.
D. $0,70$.
Nhận thấy kết quả bài toán không đổi khi ta tịnh tiến đồ thị $\left( C \right)$ sang bên trái sao cho đường thẳng $d:x={{x}_{2}}$ trùng với trục tung khi đó $\left( C \right)$ là đồ thị của hàm trùng phương $y=g\left( x \right)$ có ba điểm cực trị ${{x}_{1}}=-1,{{x}_{2}}=0,{{x}_{3}}=1$. Suy ra $y=g\left( x \right)=k\left( {{x}^{4}}-2{{x}^{2}} \right)+c \left( k>0 \right)$ Lại có $f\left( {{x}_{1}} \right)+f\left( {{x}_{3}} \right)+\dfrac{2}{3}f\left( {{x}_{2}} \right)=0\Rightarrow -2k+2c+\dfrac{2}{3}c=0\Leftrightarrow c=\dfrac{3}{4}k$
Suy ra: $y=g\left( x \right)=k\left( {{x}^{4}}-2{{x}^{2}} \right)+\dfrac{3}{4}k$
Khi đó: ${{S}_{1}}+{{S}_{2}}=k\int\limits_{0}^{1}{\left| {{x}^{4}}-2{{x}^{2}}+\dfrac{3}{4} \right|}\text{d}x=\dfrac{28\sqrt{2}-17}{60}k$.
Ta lại có: $g\left( 0 \right)-g\left( 1 \right)=k$ $\Rightarrow {{S}_{1}}+{{S}_{2}}+{{S}_{3}}+{{S}_{4}}=k.1=k$.
Suy ra ${{S}_{3}}+{{S}_{4}}=k-\dfrac{28\sqrt{2}-17}{60}k=\dfrac{77-28\sqrt{2}}{60}k\Rightarrow \dfrac{{{S}_{1}}+{{S}_{2}}}{{{S}_{3}}+{{S}_{4}}}=\dfrac{28\sqrt{2}-17}{77-28\sqrt{2}}\approx 0,604$
Đáp án A.