Google
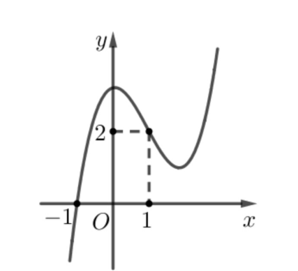
Câu hỏi: Cho hàm số bậc bốn $f(x)$ có đồ thị của đạo hàm như hình vẽ:
Trên khoảng $\left(-\dfrac{\pi}{2} ; 5 \pi\right)$, hàm số $g(x)=f(\sin x-1)+\dfrac{1}{4} \cos 2 x$ có bao nhiêu điểm cực tiểu?
A. $6$
B. $4$
C. $7$
D. $5$
A. $6$
B. $4$
C. $7$
D. $5$
Ta có
${g}'(x)=\cos x\cdot {f}'(\sin x-1)-\dfrac{1}{2}\sin 2x\text{ =}\cos x\left[ {f}'(\sin x-1)-\sin x \right]$
$\text{=}\cos x\left[ {f}'(\sin x-1)-(\sin x-1+1) \right]$
sVẽ thêm đường thẳng $y=x+1$.
Ta thấy ${f}'(x)-(x+1)$ cùng dấu với $(x+1)(x-1)(x-a),(a>1)$ nên ${g}'(x)$ cùng dấu với
$\cos x(\sin x-1+1)(\sin x-1-1)(\sin x-1-a)=\cos x \sin x \underbrace{(\sin x-2)(\sin x-(1+a))}_{>0}$
Vì $\cos x \sin x=\dfrac{1}{2} \sin 2 x$ và $\sin 2x$ đổi dấu từ âm sang dương 5 lần trên khoảng $\left(-\dfrac{\pi}{2} ; 5 \pi\right)$
nên hàm số đã cho có 5 điểm cực tiểu.
${g}'(x)=\cos x\cdot {f}'(\sin x-1)-\dfrac{1}{2}\sin 2x\text{ =}\cos x\left[ {f}'(\sin x-1)-\sin x \right]$
$\text{=}\cos x\left[ {f}'(\sin x-1)-(\sin x-1+1) \right]$
Ta thấy ${f}'(x)-(x+1)$ cùng dấu với $(x+1)(x-1)(x-a),(a>1)$ nên ${g}'(x)$ cùng dấu với
$\cos x(\sin x-1+1)(\sin x-1-1)(\sin x-1-a)=\cos x \sin x \underbrace{(\sin x-2)(\sin x-(1+a))}_{>0}$
nên hàm số đã cho có 5 điểm cực tiểu.
Đáp án D.