Google
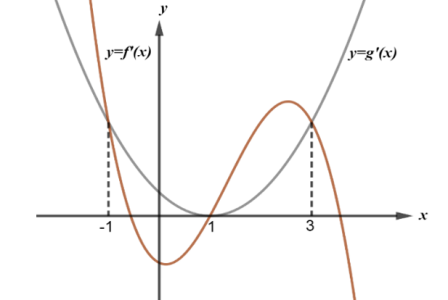
Câu hỏi: Cho hàm số bậc bốn $f\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+dx+e$ $\left( a,b,c,d,e\in \mathbb{R} \right)$ và hàm số bậc ba $g\left( x \right)=m{{x}^{3}}+n{{x}^{2}}+px+q$ $\left( m,n,p,q\in \mathbb{R} \right)$ có đồ thị $y={f}'\left( x \right)$ và $y={g}'\left( x \right)$ như hình vẽ bên dưới.
Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $y={f}'\left( x \right)$ và $y={g}'\left( x \right)$ bằng 96 và $f\left( 2 \right)=g\left( 2 \right)$. Diện tích hình phẳng giới hạn bởi các đường $y=f\left( x \right),y=g\left( x \right)$ và $x=0,x=2$ bằng
A. $\dfrac{136}{15}$.
B. $\dfrac{272}{15}$.
C. $\dfrac{68}{15}$.
D. $\dfrac{136}{5}$.
A. $\dfrac{136}{15}$.
B. $\dfrac{272}{15}$.
C. $\dfrac{68}{15}$.
D. $\dfrac{136}{5}$.
Xét hàm số $h\left( x \right)=f\left( x \right)-g\left( x \right)=a{{x}^{4}}+\left( b-m \right){{x}^{3}}+\left( c-n \right){{x}^{2}}+\left( d-p \right)x+\left( e-q \right)$
Có ${h}'\left( x \right)={f}'\left( x \right)-{g}'\left( x \right)=4a{{x}^{3}}+3\left( b-m \right){{x}^{2}}+2\left( c-n \right)x+\left( d-p \right)$
Dựa vào đồ thị hàm số ta có phương trình ${f}'\left( x \right)={g}'\left( x \right)\Leftrightarrow {f}'\left( x \right)-{g}'\left( x \right)=0$ có ba nghiệm phân biệt $\left[ \begin{aligned}
& {{x}_{1}}=-1 \\
& {{x}_{2}}=1 \\
& {{x}_{3}}=3 \\
\end{aligned} \right.$.
Ta có ${h}'\left( x \right)={f}'\left( x \right)-{g}'\left( x \right)=4a\left( x+1 \right)\left( x-1 \right)\left( x-3 \right)=4a\left( {{x}^{3}}-3{{x}^{2}}-x+3 \right)$ với $a<0$
Suy ra $h\left( x \right)=f\left( x \right)-g\left( x \right)=4a\left( \dfrac{{{x}^{4}}}{4}-{{x}^{3}}-\dfrac{{{x}^{2}}}{2}+3x \right)+\left( e-q \right)$
Có $f\left( 2 \right)=g\left( 2 \right)\Leftrightarrow f\left( 2 \right)-g\left( 2 \right)=0\Leftrightarrow (e-q)=0$
Suy ra $h\left( x \right)=f\left( x \right)-g\left( x \right)=4a\left( \dfrac{{{x}^{4}}}{4}-{{x}^{3}}-\dfrac{{{x}^{2}}}{2}+3x \right)$
Gọi S là diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $y={f}'\left( x \right)$ và $y={g}'\left( x \right)$. Khi đó:
$S=\int\limits_{-1}^{3}{\left| 4a\left( {{x}^{3}}-3{{x}^{2}}-x+3 \right) \right|}\text{d}x=96$
$\Leftrightarrow \left| 4a \right|\int\limits_{-1}^{3}{\left| {{x}^{3}}-3{{x}^{2}}-x+3 \right|}\text{d}x=96$
$\Leftrightarrow \left| 4a \right|.8=96\Leftrightarrow a=-3$
Vậy diện tích hình phẳng giới hạn bỏi các đường $y=f\left( x \right),y=g\left( x \right)$ và $x=0,x=2$ bằng
$S=\int\limits_{0}^{2}{\left| 4.\left( -3 \right)\left( \dfrac{{{x}^{4}}}{4}-{{x}^{3}}-\dfrac{{{x}^{2}}}{2}+3x \right) \right|}\text{d}x=\dfrac{136}{5}$
Có ${h}'\left( x \right)={f}'\left( x \right)-{g}'\left( x \right)=4a{{x}^{3}}+3\left( b-m \right){{x}^{2}}+2\left( c-n \right)x+\left( d-p \right)$
Dựa vào đồ thị hàm số ta có phương trình ${f}'\left( x \right)={g}'\left( x \right)\Leftrightarrow {f}'\left( x \right)-{g}'\left( x \right)=0$ có ba nghiệm phân biệt $\left[ \begin{aligned}
& {{x}_{1}}=-1 \\
& {{x}_{2}}=1 \\
& {{x}_{3}}=3 \\
\end{aligned} \right.$.
Ta có ${h}'\left( x \right)={f}'\left( x \right)-{g}'\left( x \right)=4a\left( x+1 \right)\left( x-1 \right)\left( x-3 \right)=4a\left( {{x}^{3}}-3{{x}^{2}}-x+3 \right)$ với $a<0$
Suy ra $h\left( x \right)=f\left( x \right)-g\left( x \right)=4a\left( \dfrac{{{x}^{4}}}{4}-{{x}^{3}}-\dfrac{{{x}^{2}}}{2}+3x \right)+\left( e-q \right)$
Có $f\left( 2 \right)=g\left( 2 \right)\Leftrightarrow f\left( 2 \right)-g\left( 2 \right)=0\Leftrightarrow (e-q)=0$
Suy ra $h\left( x \right)=f\left( x \right)-g\left( x \right)=4a\left( \dfrac{{{x}^{4}}}{4}-{{x}^{3}}-\dfrac{{{x}^{2}}}{2}+3x \right)$
Gọi S là diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $y={f}'\left( x \right)$ và $y={g}'\left( x \right)$. Khi đó:
$S=\int\limits_{-1}^{3}{\left| 4a\left( {{x}^{3}}-3{{x}^{2}}-x+3 \right) \right|}\text{d}x=96$
$\Leftrightarrow \left| 4a \right|\int\limits_{-1}^{3}{\left| {{x}^{3}}-3{{x}^{2}}-x+3 \right|}\text{d}x=96$
$\Leftrightarrow \left| 4a \right|.8=96\Leftrightarrow a=-3$
Vậy diện tích hình phẳng giới hạn bỏi các đường $y=f\left( x \right),y=g\left( x \right)$ và $x=0,x=2$ bằng
$S=\int\limits_{0}^{2}{\left| 4.\left( -3 \right)\left( \dfrac{{{x}^{4}}}{4}-{{x}^{3}}-\dfrac{{{x}^{2}}}{2}+3x \right) \right|}\text{d}x=\dfrac{136}{5}$
Đáp án D.