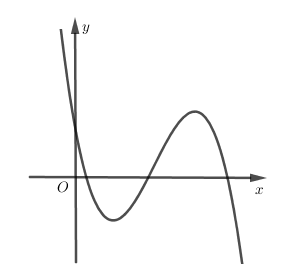
Cho hàm số bậc bốn $f\left( x \right).$ Hàm số $y={f}'\left( x...

${f}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=a \\
& x=b \\
& x=c \\
\end{aligned} \right. ; \left( a<b<c \right)$.
Từ đồ thị của hàm số $y={f}'\left( x \right)$ ta có bảng biến thiên như sau
Vậy hàm số $f\left( x \right)$ có 2 điểm cực đại.