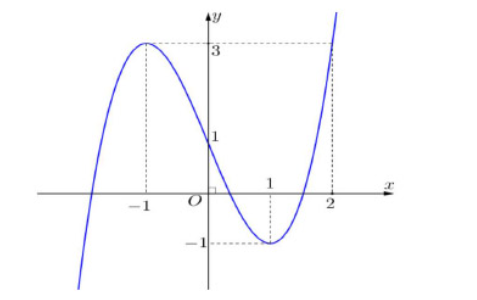
Câu hỏi: Cho hàm số bậc ba ${y=f(x)}$ có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình ${f(f(x))=1}$ là
A. 9 .
B. 7 .
C. 3 .
D. 6 .

Ta có: ${f(f(x))=1 \Leftrightarrow\left[\begin{array}{ll}f(x) & =0 \\ f(x) & =a \\ f(x) & =b \quad(a<-1) \\ (1<b<2)\end{array}\right.}$
Ta dựa vào đồ thị:
Phương trình ${f(x)=0}$ có 3 nghiệm. Phương trình ${f(x)=a}$ có 1 nghiệm.
Phương trình ${f(x)=b}$ có 3 nghiệm.
Vậy phương trình ${f(f(x))=1}$ có 7 nghiệm phân biệt.

A. 9 .
B. 7 .
C. 3 .
D. 6 .
Ta có: ${f(f(x))=1 \Leftrightarrow\left[\begin{array}{ll}f(x) & =0 \\ f(x) & =a \\ f(x) & =b \quad(a<-1) \\ (1<b<2)\end{array}\right.}$
Ta dựa vào đồ thị:
Phương trình ${f(x)=0}$ có 3 nghiệm. Phương trình ${f(x)=a}$ có 1 nghiệm.
Phương trình ${f(x)=b}$ có 3 nghiệm.
Vậy phương trình ${f(f(x))=1}$ có 7 nghiệm phân biệt.
Đáp án B.