Cho hàm số bậc ba $y=f\left(x\right)$ có đồ thị như hình vẽ...

Ta có: $g^{\prime }\left(x\right)={\displaystyle \frac{f^{\prime }\left(x\right)(2f\left(x\right)-4)(f^2\left(x\right)-4f\left(x\right)-m)}{|f^2\left(x\right)-4f\left(x\right)-m|}}.f^{\prime }\left(|f^2\left(x\right)-4f\left(x\right)-m|\right)=0$
$\iff [\begin{array}{c}{f}^{\prime }\left(x\right)=0\left(1\right)\\ 2f\left(x\right)-4=0\iff f\left(x\right)=2\left(2\right)\\ f^2\left(x\right)-4f\left(x\right)-m=0\iff f^2\left(x\right)-4f\left(x\right)=m\left(3\right)\\ |f^2\left(x\right)-4f\left(x\right)-m|=-1\left(voly\right)\\ |f^2\left(x\right)-4f\left(x\right)-m|=2\iff [\begin{array}{c}{f}^2\left(x\right)-4f\left(x\right)-m=2\\ f^2\left(x\right)-4f\left(x\right)-m=-2\end{array}\iff [\begin{array}{c}{f}^2\left(x\right)-4f\left(x\right)=m+2\left(4\right)\\ f^2\left(x\right)-4f\left(x\right)=m-2\left(5\right)\end{array}\end{array}$
Dễ thấy $\left(1\right)$ có 2 nghiệm đơn (vì có 2 cực trị) và $\left(2\right)$ có 3 nghiệm đơn
Vậy tổng số nghiệm đơn của phương trình $\left(3\right);\left(4\right);\left(5\right)$ là 12 thì thỏa mãn
Đặt $u=u\left(x\right)=f^2\left(x\right)-4f\left(x\right)\Rightarrow u^{\prime }=2f^{\prime }\left(x\right)(f\left(x\right)-2)\Rightarrow u^{\prime }=0\iff [\begin{array}{rl}& x\in \{-1;2\}\\ & x\in \{a;b;c\}\end{array}$.
Các nghiệm trên được sắp thứ tự từ nhỏ đến lớn như sau: $a<-1<b<2<c$.
Bảng biến thiên của hàm số $u=f^2\left(x\right)-4f\left(x\right)$.
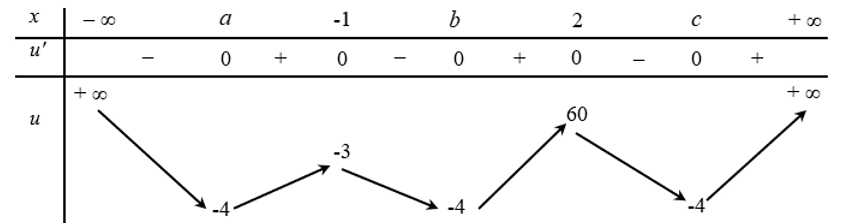Vậy số giao điểm của các đường thẳng $y=m-2;y=m;y=m+2$ với đồ thị $u\left(x\right)$ là 12 điểm phân biệt $\iff \{\begin{array}{rl}& -3\le m-2<60\\ & -3\le m+2<60\end{array}\iff -1\le m<58\Rightarrow m\in \{-1;0;1;...;57\}\Rightarrow S=1652$.