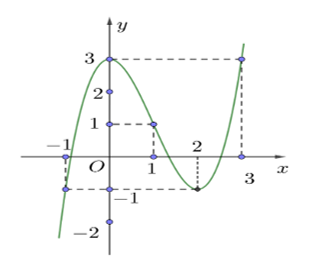
Cho hàm số bậc ba $y=f\left( x \right)$ có đồ thị như hình vẽ bên...

Phương trình $\left| f\left( {{x}^{4}}-2{{x}^{2}} \right) \right|=2\Leftrightarrow \left[ \begin{aligned}
& f\left( {{x}^{4}}-2{{x}^{2}} \right)=2 \\
& f\left( {{x}^{4}}-2{{x}^{2}} \right)=-2 \\
\end{aligned} \right.$
* Phương trình $f\left( {{x}^{4}}-2{{x}^{2}} \right)=2\Leftrightarrow \left[ \begin{aligned}
& {{x}^{4}}-2{{x}^{2}}=b, \left( -1<b<0 \right) \\
& {{x}^{4}}-2{{x}^{2}}=c, \left( 0<c<1 \right) \\
& {{x}^{4}}-2{{x}^{2}}=d, \left( 2<d<3 \right) \\
\end{aligned} \right.$.
* Phương trình $f\left( {{x}^{4}}-2{{x}^{2}} \right)=-2\Leftrightarrow {{x}^{4}}-2{{x}^{2}}=a, \left( -2<a<-1 \right)$.
Bảng biến thiên của hàm số $y={{x}^{4}}-2{{x}^{2}}$ như sau:
Dựa vào BBT trên ta có:
- Phương trình ${{x}^{4}}-2{{x}^{2}}=a, \left( -2<a<-1 \right)$ không có nghiệm thực.
- Phương trình ${{x}^{4}}-2{{x}^{2}}=b, \left( -1<b<0 \right)$ có 4 nghiệm thực phân biệt.
- Phương trình ${{x}^{4}}-2{{x}^{2}}=c, \left( 0<c<1 \right)$ có 2 nghiệm thực phân biệt.
- Phương trình ${{x}^{4}}-2{{x}^{2}}=d, \left( 2<d<3 \right)$ có 2 nghiệm thực phân biệt.
Vậy phương trình $\left| f\left( {{x}^{4}}-2{{x}^{2}} \right) \right|=2$ có 8 nghiệm thực phân biệt.