Google
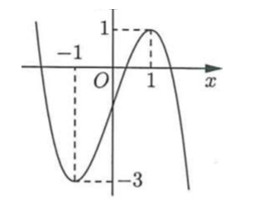
Câu hỏi: Cho hàm số bậc ba $y=f\left( x \right)$ có đồ thị là đường cong như hình bên dưới.
Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $2f(x)=m$ có ba nghiệm thực phân biệt?
A. $9$.
B. $5$.
C. $7$.
D. $3$.
A. $9$.
B. $5$.
C. $7$.
D. $3$.
Xét phương trình: $2f(x)=m\Leftrightarrow f(x)=\dfrac{m}{2}$.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số $y=f(x)$ và đường thẳng $y=\dfrac{m}{2}$.
Dựa vào đồ thị ta có điều kiện để phương trình có ba nghiệm phân biệt là:
$-3<\dfrac{m}{2}<1\Leftrightarrow -6<m<2$
$m\in \mathbb{Z}; m\in \left\{ -5;-4;-3;-2;-1;0;1 \right\}$
Có 7 giá trị nguyên của m thỏa mãn điều kiện.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số $y=f(x)$ và đường thẳng $y=\dfrac{m}{2}$.
Dựa vào đồ thị ta có điều kiện để phương trình có ba nghiệm phân biệt là:
$-3<\dfrac{m}{2}<1\Leftrightarrow -6<m<2$
$m\in \mathbb{Z}; m\in \left\{ -5;-4;-3;-2;-1;0;1 \right\}$
Có 7 giá trị nguyên của m thỏa mãn điều kiện.
Đáp án C.