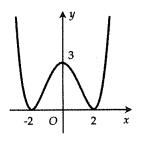
Câu hỏi: Cho hàm số bậc 4 trùng phương $y=f\left( x \right)$ có đồ thị là đường cong hình bên. Đồ thị hàm số $g\left( x \right)=\dfrac{2019{{\left( x-2 \right)}^{3}}\sqrt{{{x}^{2}}+2020}}{f\left( x \right)}$ có tất cả bao nhiêu đường tiệm cận?
A. 2.
B. 4.
C. 3.
D. 5.

A. 2.
B. 4.
C. 3.
D. 5.
Tập xác định: $\mathbb{R}\backslash \left\{ 2;-2 \right\}$.
Dựa vào đồ thị ta thấy $f\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=-2 \\
& x=2 \\
\end{aligned} \right.$.
$\underset{x\to 2}{\mathop{\lim }} g\left( x \right)=\underset{x\to 2}{\mathop{\lim }} \dfrac{2019{{\left( x-2 \right)}^{3}}\sqrt{{{x}^{2}}+2020}}{f\left( x \right)}=0$,
$\underset{x\to {{\left( -2 \right)}^{+}}}{\mathop{\lim }} g\left( x \right)=\underset{x\to {{\left( -2 \right)}^{+}}}{\mathop{\lim }} \dfrac{2019{{\left( x-2 \right)}^{3}}\sqrt{{{x}^{2}}+2020}}{f\left( x \right)}=+\infty $.
Suy ra đồ thị hàm số $y=g\left( x \right)$ có một đường tiệm đứng: $x=-2$.
Vì $y=f\left( x \right)$ là hàm số bậc 4 trùng phương nên giả sử $f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c\left( a>0 \right)$
Ta có $\underset{x\to +\infty }{\mathop{\lim }} g\left( x \right)=\dfrac{2019}{a}$ và $\underset{x\to -\infty }{\mathop{\lim }} g\left( x \right)=-\dfrac{2019}{a}$.
Do đó đồ thị hàm số $y=g\left( x \right)$ có hai đường tiệm cận ngang $y=\dfrac{2019}{a};y=-\dfrac{2019}{a}$.
Dựa vào đồ thị ta thấy $f\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=-2 \\
& x=2 \\
\end{aligned} \right.$.
$\underset{x\to 2}{\mathop{\lim }} g\left( x \right)=\underset{x\to 2}{\mathop{\lim }} \dfrac{2019{{\left( x-2 \right)}^{3}}\sqrt{{{x}^{2}}+2020}}{f\left( x \right)}=0$,
$\underset{x\to {{\left( -2 \right)}^{+}}}{\mathop{\lim }} g\left( x \right)=\underset{x\to {{\left( -2 \right)}^{+}}}{\mathop{\lim }} \dfrac{2019{{\left( x-2 \right)}^{3}}\sqrt{{{x}^{2}}+2020}}{f\left( x \right)}=+\infty $.
Suy ra đồ thị hàm số $y=g\left( x \right)$ có một đường tiệm đứng: $x=-2$.
Vì $y=f\left( x \right)$ là hàm số bậc 4 trùng phương nên giả sử $f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c\left( a>0 \right)$
Ta có $\underset{x\to +\infty }{\mathop{\lim }} g\left( x \right)=\dfrac{2019}{a}$ và $\underset{x\to -\infty }{\mathop{\lim }} g\left( x \right)=-\dfrac{2019}{a}$.
Do đó đồ thị hàm số $y=g\left( x \right)$ có hai đường tiệm cận ngang $y=\dfrac{2019}{a};y=-\dfrac{2019}{a}$.
Đáp án C.