Google
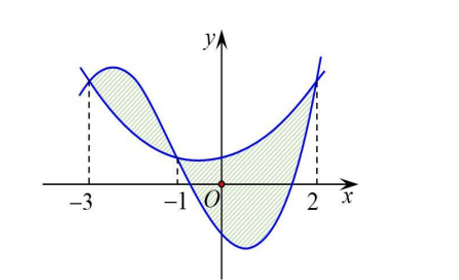
Câu hỏi: Cho hai hàm số $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx-1$ và $g\left( x \right)=d{{x}^{2}}+ex+\dfrac{1}{2}$ ( $a$, $b$, $c$, $d$, $e\in \mathbb{R}$ ). Biết rằng đồ thị của hàm số $y=f\left( x \right)$ và $y=g\left( x \right)$ cắt nhau tại ba điểm có hoành độ lần lượt $-3$ ; $-1$ ; $2$ (tham khảo hình vẽ).
Hình phẳng giới hạn bởi hai đồ thị hàm số đã cho có diện tích bằng
A. $\dfrac{125}{12}$.
B. $\dfrac{253}{48}$.
C. $\dfrac{253}{24}$.
D. $\dfrac{253}{12}$.
A. $\dfrac{125}{12}$.
B. $\dfrac{253}{48}$.
C. $\dfrac{253}{24}$.
D. $\dfrac{253}{12}$.
Vì đồ thị của hai hàm số $y=f\left( x \right)$ và $y=g\left( x \right)$ cắt nhau tại các điểm có hoành độ lần lượt bằng $-3$, $-1$, $2$ nên phương trình $f\left( x \right)-g\left( x \right)=0$ có ba nghiệm phân biệt là $-3$, $-1$, $2$.
Do đó, $f\left( x \right)-g\left( x \right)=a\left( x+3 \right)(x+1)(x-2)$.
$\Rightarrow -6a=f\left( 0 \right)-g\left( 0 \right)=-1-\dfrac{1}{2}$
$\Rightarrow a=\dfrac{1}{4}$.
Diện tích hình phẳng giới hạn bởi hai đường $y=f\left( x \right)$ và $y=g\left( x \right)$ là
$S=\int\limits_{-3}^{2}{\left| f\left( x \right)-g\left( x \right) \right|}\text{d}x=\int\limits_{-3}^{2}{\left| \dfrac{1}{4}\left( x+3 \right)(x+1)(x-2) \right|}\text{d}x=\dfrac{253}{48}$.
Do đó, $f\left( x \right)-g\left( x \right)=a\left( x+3 \right)(x+1)(x-2)$.
$\Rightarrow -6a=f\left( 0 \right)-g\left( 0 \right)=-1-\dfrac{1}{2}$
$\Rightarrow a=\dfrac{1}{4}$.
Diện tích hình phẳng giới hạn bởi hai đường $y=f\left( x \right)$ và $y=g\left( x \right)$ là
$S=\int\limits_{-3}^{2}{\left| f\left( x \right)-g\left( x \right) \right|}\text{d}x=\int\limits_{-3}^{2}{\left| \dfrac{1}{4}\left( x+3 \right)(x+1)(x-2) \right|}\text{d}x=\dfrac{253}{48}$.
Đáp án B.