Cho hai hàm số $f\left( x \right)=2{{x}^{3}}-9{{x}^{2}}$ và...

Ta có: $h\left( x \right)=f\left( g\left( x \right) \right)\Rightarrow {h}'\left( x \right)={g}'\left( x \right).{f}'\left( g\left( x \right) \right)\Rightarrow {h}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& {g}'\left( x \right)=0 \\
& {f}'\left( g\left( x \right) \right)=0 \\
\end{aligned} \right.$
• ${g}'\left( x \right)=0\Leftrightarrow 6{{x}^{2}}-6x-12=0\Leftrightarrow \left[ \begin{aligned}
& x=-1 \\
& x=2 \\
\end{aligned} \right.$
• ${f}'\left( g\left( x \right) \right)=\left[ \begin{aligned}
& g\left( x \right)=0 \\
& g\left( x \right)=3 \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& 2{{x}^{3}}-3{{x}^{2}}-12=-m \\
& 2{{x}^{3}}-2{{x}^{2}}-12=-m+3 \\
\end{aligned} \right.\left( 1 \right)$
Vẽ bảng biến thiên của hàm số $g\left( x \right)$ như sau:

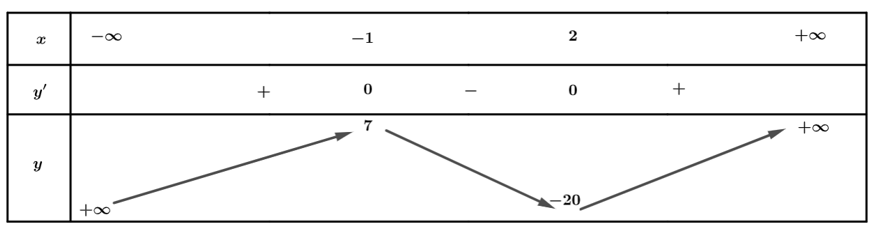
Để hàm số $h\left( x \right)$ có $6$ điểm cực trị thì $\left( 1 \right)$ phải có $4$ nghiệm nên:
$\left[ \begin{aligned}
& \left\{ \begin{aligned}
& -m+3>7 \\
& -20<-m\le 7 \\
\end{aligned} \right. \\
& \left\{ \begin{aligned}
& -m\le -20 \\
& -20<-m+3<7 \\
\end{aligned} \right. \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& -7<m\le -4 \\
& 20\le m<23 \\
\end{aligned} \right.$
Vậy có $6$ giá trị nguyên của tham số $m$ thỏa mãn yêu cầu bài toán.