Google
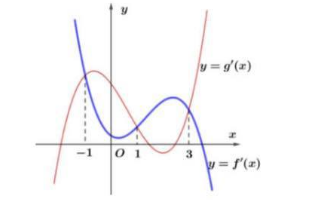
Câu hỏi: Cho hai hàm số bậc bốn $f(x), g(x)$ có đồ thị $y=f^{\prime}(x)$ và $y=g^{\prime}(x)$ như hình vẽ
Số giá trị thực của tham số $m$ để phương trình $f(x)-g(x)=m$ có một nghiệm duy nhất trên $[-1 ; 3]$ là
A. $5$.
B. $0.$
C. $2.$
D. $1.$
A. $5$.
B. $0.$
C. $2.$
D. $1.$
Dựa vào đồ thị ta có
${f}'(x)-{g}'(x)=a\left( x+1 \right)\left( x-1 \right)\left( x-3 \right)\Rightarrow \int{\left( {f}'(x)-{g}'(x) \right)}dx=a\int{\left( {{x}^{3}}-3{{x}^{2}}-x+3 \right)}dx$
$\Rightarrow f(x)-g(x)=a\left( \dfrac{{{x}^{4}}}{4}-{{x}^{3}}-\dfrac{{{x}^{2}}}{2}+3x \right)+b$, $\left( a<0 \right)$
Đặt $h\left( x \right)=f(x)-g(x)\Rightarrow {h}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=-1 \\
& x=1 \\
& x=3 \\
\end{aligned} \right..$
Ta có bảng biến thiên của $y=h\left( x \right)$
Để phương trình $f(x)-g(x)=m$ có nghiệm duy nhất trên $[-1 ; 3]$ thì chỉ có duy nhất
$1$ giá trị của $m.$
${f}'(x)-{g}'(x)=a\left( x+1 \right)\left( x-1 \right)\left( x-3 \right)\Rightarrow \int{\left( {f}'(x)-{g}'(x) \right)}dx=a\int{\left( {{x}^{3}}-3{{x}^{2}}-x+3 \right)}dx$
$\Rightarrow f(x)-g(x)=a\left( \dfrac{{{x}^{4}}}{4}-{{x}^{3}}-\dfrac{{{x}^{2}}}{2}+3x \right)+b$, $\left( a<0 \right)$
Đặt $h\left( x \right)=f(x)-g(x)\Rightarrow {h}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=-1 \\
& x=1 \\
& x=3 \\
\end{aligned} \right..$
Ta có bảng biến thiên của $y=h\left( x \right)$
$1$ giá trị của $m.$
Đáp án D.