Google
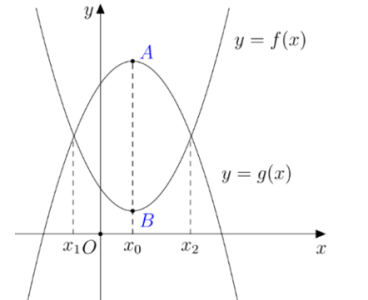
Câu hỏi: Cho hai hàm đa thức $y=f\left( x \right),y=g\left( x \right)$ liên tục trên $\mathbb{R}$, có đồ thị là hai đường cong như hình bên dưới. Biết rằng đồ thị hàm số $y=f\left( x \right)$ có đúng một cực trị là $A$, đồ thị hàm số $y=g\left( x \right)$ có đúng một điểm cực trị là $B$ và $AB=10$.
Số giá trị nguyên của tham số $m$ để hàm số $y=\left| \left| f\left( x \right)-g\left( x \right) \right|-\dfrac{2m}{3}-4 \right|$ có đúng $7$ điểm cực trị là.
A. $10$.
B. $20$.
C. $25$.
D. $14$.
A. $10$.
B. $20$.
C. $25$.
D. $14$.
Ta có hàm số $y=f\left( x \right)$ có đúng một cực trị là $A,x={{x}_{0}}$, đồ thị hàm số $y=g\left( x \right)$ có đúng một điểm cực trị là $B,x={{x}_{0}}$ nên ${f}'\left( {{x}_{0}} \right)=0,{g}'\left( {{x}_{0}} \right)=0$.
Xét hàm số $h\left( x \right)=f\left( x \right)-g\left( x \right)\Rightarrow {h}'\left( x \right)={f}'\left( x \right)-{g}'\left( x \right)$
Khi đó ${h}'\left( x \right)=0\Leftrightarrow {f}'\left( x \right)-{g}'\left( x \right)=0\Leftrightarrow x={{x}_{0}}$
Lại có $h\left( {{x}_{0}} \right)=0\Leftrightarrow f\left( {{x}_{0}} \right)-g\left( {{x}_{0}} \right)={{y}_{B}}-{{y}_{A}}=-10\left( AB=10 \right)$
$h\left( x \right)=0\Leftrightarrow f\left( x \right)-g\left( x \right)=0\Leftrightarrow f\left( x \right)=g\left( x \right)\Leftrightarrow \left[ \begin{aligned}
& x={{x}_{1}} \\
& x={{x}_{2}} \\
\end{aligned} \right.$
Bảng biến thiên của hàm số $h\left( x \right)$ là
Suy ra bảng biến thiên của hàm số $\left| h\left( x \right) \right|$ là
Từ BBT suy ra số cực trị của hàm số $\left| h\left( x \right) \right|$ là 3 cực trị thì số cực trị của hàm số $\left| h\left( x \right) \right|-\dfrac{2m}{3}-4$ cũng là 3 cực trị.
Lại có số cực trị của hàm số $y=\left| \left| h\left( x \right) \right|-\dfrac{2m}{3}-4 \right|$ bằng tổng số số điểm cực trị của hàm số $\left| h\left( x \right) \right|-\dfrac{2m}{3}-4$ và số nghiệm đơn (hay bội lẻ) của phương trình $\left| h\left( x \right) \right|-\dfrac{2m}{3}-4=0$
Nên hàm số $y=\left| \left| h\left( x \right) \right|-\dfrac{2m}{3}-4 \right|$
có đúng $7$ cực trị thì phương trình $\left| h\left( x \right) \right|-\dfrac{2m}{3}-4=0\Leftrightarrow \left| h\left( x \right) \right|=\dfrac{2m}{3}+4$ có đúng $4$ nghiệm đơn (hay bội lẻ)
Từ BBT suy ra $0<\dfrac{2m}{3}+4<10\Leftrightarrow -6<m<9$ mà $m\in \mathbb{Z}\Rightarrow m\in \left\{ -5;-4;-3;-2;-1;0;1;2;3;4;5;6;7;8 \right\}$
Vậy có $14$ giá trị m thỏa mãn.
Xét hàm số $h\left( x \right)=f\left( x \right)-g\left( x \right)\Rightarrow {h}'\left( x \right)={f}'\left( x \right)-{g}'\left( x \right)$
Khi đó ${h}'\left( x \right)=0\Leftrightarrow {f}'\left( x \right)-{g}'\left( x \right)=0\Leftrightarrow x={{x}_{0}}$
Lại có $h\left( {{x}_{0}} \right)=0\Leftrightarrow f\left( {{x}_{0}} \right)-g\left( {{x}_{0}} \right)={{y}_{B}}-{{y}_{A}}=-10\left( AB=10 \right)$
$h\left( x \right)=0\Leftrightarrow f\left( x \right)-g\left( x \right)=0\Leftrightarrow f\left( x \right)=g\left( x \right)\Leftrightarrow \left[ \begin{aligned}
& x={{x}_{1}} \\
& x={{x}_{2}} \\
\end{aligned} \right.$
Bảng biến thiên của hàm số $h\left( x \right)$ là
Lại có số cực trị của hàm số $y=\left| \left| h\left( x \right) \right|-\dfrac{2m}{3}-4 \right|$ bằng tổng số số điểm cực trị của hàm số $\left| h\left( x \right) \right|-\dfrac{2m}{3}-4$ và số nghiệm đơn (hay bội lẻ) của phương trình $\left| h\left( x \right) \right|-\dfrac{2m}{3}-4=0$
Nên hàm số $y=\left| \left| h\left( x \right) \right|-\dfrac{2m}{3}-4 \right|$
có đúng $7$ cực trị thì phương trình $\left| h\left( x \right) \right|-\dfrac{2m}{3}-4=0\Leftrightarrow \left| h\left( x \right) \right|=\dfrac{2m}{3}+4$ có đúng $4$ nghiệm đơn (hay bội lẻ)
Từ BBT suy ra $0<\dfrac{2m}{3}+4<10\Leftrightarrow -6<m<9$ mà $m\in \mathbb{Z}\Rightarrow m\in \left\{ -5;-4;-3;-2;-1;0;1;2;3;4;5;6;7;8 \right\}$
Vậy có $14$ giá trị m thỏa mãn.
Đáp án D.