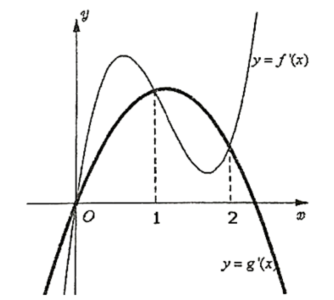
Câu hỏi: Cho hai đồ thị hàm số $f\left( x \right)$ và $g\left( x \right)$ liên tục trên $\mathbb{R}$ và hàm số ${f}'\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$, ${g}'\left( x \right)=q{{x}^{2}}+nx+p$ với $a,q\ne 0$ có đồ thị như hình vẽ. Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $y={f}'\left( x \right)$ và $y={g}'\left( x \right)$ bằng $10$ và $f\left( 2 \right)=g\left( 2 \right)$. Tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $y=f\left( x \right)$ và $y=g\left( x \right)$.
A. $\dfrac{8}{3}$.
B. $\dfrac{16}{3}$.
C. $\dfrac{8}{15}$.
D. $\dfrac{16}{5}$.
A. $\dfrac{8}{3}$.
B. $\dfrac{16}{3}$.
C. $\dfrac{8}{15}$.
D. $\dfrac{16}{5}$.
Ta có: ${f}'\left( x \right)-{g}'\left( x \right)=4a\left( {{x}^{3}}-3{{x}^{2}}+2x \right) \left( a>0 \right)\Rightarrow 4a\int\limits_{0}^{2}{\left| {{x}^{3}}-3{{x}^{2}}+2x \right|\text{d}x}=\dfrac{4a}{2}=10\Rightarrow a=5$. $\Rightarrow {f}'\left( x \right)-{g}'\left( x \right)=20\left( {{x}^{3}}-3{{x}^{2}}+2x \right)\Rightarrow f\left( x \right)-g\left( x \right)=5{{x}^{4}}-20{{x}^{3}}+20{{x}^{2}}+C$.
$f\left( 2 \right)-g\left( 2 \right)=0\Rightarrow C=0\Rightarrow f\left( x \right)-g\left( x \right)=5{{x}^{4}}-20{{x}^{3}}+20{{x}^{2}}\Rightarrow f\left( x \right)-g\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=0 \\
& x=2 \\
\end{aligned} \right.$.
Vậy $S=5\int\limits_{0}^{2}{{{x}^{2}}{{\left( x-2 \right)}^{2}}\text{d}x}=\dfrac{16}{3}$.
$f\left( 2 \right)-g\left( 2 \right)=0\Rightarrow C=0\Rightarrow f\left( x \right)-g\left( x \right)=5{{x}^{4}}-20{{x}^{3}}+20{{x}^{2}}\Rightarrow f\left( x \right)-g\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=0 \\
& x=2 \\
\end{aligned} \right.$.
Vậy $S=5\int\limits_{0}^{2}{{{x}^{2}}{{\left( x-2 \right)}^{2}}\text{d}x}=\dfrac{16}{3}$.
Đáp án B.