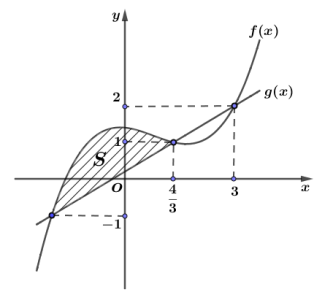
Câu hỏi: Cho $f\left( x \right),g\left( x \right)$ lần lượt là các hàm số đa thức bậc ba và bậc nhất có đồ thị như hình vẽ. Biết diện tích $S$ (được đánh dấu) bằng $\dfrac{250}{81}$. Tính $\int\limits_{0}^{1}{f\left( x \right)}\text{d}x$.
A. $\dfrac{34}{27}$.
B. $\dfrac{61}{48}$.
C. $\dfrac{17}{15}$.
D. $\dfrac{43}{35}$.

A. $\dfrac{34}{27}$.
B. $\dfrac{61}{48}$.
C. $\dfrac{17}{15}$.
D. $\dfrac{43}{35}$.
Đồ thị hàm số $y=g\left( x \right)$ đi qua hai điểm $A\left( \dfrac{4}{3};1 \right)$ và $B\left( 3;2 \right)$ suy ra $g\left( x \right)=\dfrac{3}{5}x+\dfrac{1}{5}$.
Đồ thị hàm số $y=g\left( x \right)$ đi qua điểm $C$ có tung độ $-1$, suy ra $C\left( -2;-1 \right)$.
Đặt $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d,a\ne 0$. Đồ thị hàm số $y=f\left( x \right)$ đi qua 3 điểm $A,B,C$ nên ta có
$\left\{ \begin{aligned}
& \dfrac{64}{27}a+\dfrac{16}{9}b+\dfrac{4}{3}c+d=1 \left( 1 \right) \\
& 27a+9b+3c+d=2 \left( 2 \right) \\
& -8a+4b-2c+d=-1 \left( 3 \right) \\
\end{aligned} \right.$
Mặt khác
$\begin{aligned}
& S=\int\limits_{-2}^{\dfrac{4}{3}}{\left[ f\left( x \right)-g\left( x \right) \right]}\text{d}x=\int\limits_{-2}^{\dfrac{4}{3}}{\left[ \left( a{{x}^{3}}+b{{x}^{2}}+cx+d \right)-\left( \dfrac{3}{5}x+\dfrac{1}{5} \right) \right]}\text{d}x \\
& =\int\limits_{-2}^{\dfrac{4}{3}}{\left( a{{x}^{3}}+b{{x}^{2}}+\left( c-\dfrac{3}{5} \right)x+d-\dfrac{1}{5} \right)}\text{d}x=\left. \left( \dfrac{1}{4}a{{x}^{4}}+\dfrac{1}{3}b{{x}^{3}}+\dfrac{1}{2}\left( c-\dfrac{3}{5} \right){{x}^{2}}+\left( d-\dfrac{1}{5} \right)x \right) \right|_{-2}^{\dfrac{4}{3}} \\
& =\dfrac{1}{4}\left( \dfrac{256}{81}-16 \right)a+\dfrac{1}{3}\left( \dfrac{64}{27}+8 \right)b+\dfrac{1}{2}\left( c-\dfrac{3}{5} \right)\left( \dfrac{16}{9}-4 \right)+\left( d-\dfrac{1}{5} \right)\left( \dfrac{4}{3}+2 \right) \\
& =-\dfrac{260}{81}a+\dfrac{280}{81}b-\dfrac{10}{9}c+\dfrac{10}{3}d \\
\end{aligned}$
Suy ra $-\dfrac{260}{81}a+\dfrac{280}{81}b-\dfrac{10}{9}c+\dfrac{10}{3}d=\dfrac{250}{81} \left( 4 \right)$.
Từ $\left( 1 \right),\left( 2 \right),\left( 3 \right),\left( 4 \right)$ ta được $a=\dfrac{3}{20},b=-\dfrac{7}{20},c=-\dfrac{1}{10},d=\dfrac{7}{5}$.
Vậy $f\left( x \right)=\dfrac{3}{20}{{x}^{3}}-\dfrac{7}{20}{{x}^{2}}-\dfrac{1}{10}x+\dfrac{7}{5}$. Khi đó $f\left( x \right)=\int\limits_{0}^{1}{\left( \dfrac{3}{20}{{x}^{3}}-\dfrac{7}{20}{{x}^{2}}-\dfrac{1}{10}x+\dfrac{7}{5} \right)}\text{d}x=\dfrac{61}{48}$.
Đồ thị hàm số $y=g\left( x \right)$ đi qua điểm $C$ có tung độ $-1$, suy ra $C\left( -2;-1 \right)$.
Đặt $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d,a\ne 0$. Đồ thị hàm số $y=f\left( x \right)$ đi qua 3 điểm $A,B,C$ nên ta có
$\left\{ \begin{aligned}
& \dfrac{64}{27}a+\dfrac{16}{9}b+\dfrac{4}{3}c+d=1 \left( 1 \right) \\
& 27a+9b+3c+d=2 \left( 2 \right) \\
& -8a+4b-2c+d=-1 \left( 3 \right) \\
\end{aligned} \right.$
Mặt khác
$\begin{aligned}
& S=\int\limits_{-2}^{\dfrac{4}{3}}{\left[ f\left( x \right)-g\left( x \right) \right]}\text{d}x=\int\limits_{-2}^{\dfrac{4}{3}}{\left[ \left( a{{x}^{3}}+b{{x}^{2}}+cx+d \right)-\left( \dfrac{3}{5}x+\dfrac{1}{5} \right) \right]}\text{d}x \\
& =\int\limits_{-2}^{\dfrac{4}{3}}{\left( a{{x}^{3}}+b{{x}^{2}}+\left( c-\dfrac{3}{5} \right)x+d-\dfrac{1}{5} \right)}\text{d}x=\left. \left( \dfrac{1}{4}a{{x}^{4}}+\dfrac{1}{3}b{{x}^{3}}+\dfrac{1}{2}\left( c-\dfrac{3}{5} \right){{x}^{2}}+\left( d-\dfrac{1}{5} \right)x \right) \right|_{-2}^{\dfrac{4}{3}} \\
& =\dfrac{1}{4}\left( \dfrac{256}{81}-16 \right)a+\dfrac{1}{3}\left( \dfrac{64}{27}+8 \right)b+\dfrac{1}{2}\left( c-\dfrac{3}{5} \right)\left( \dfrac{16}{9}-4 \right)+\left( d-\dfrac{1}{5} \right)\left( \dfrac{4}{3}+2 \right) \\
& =-\dfrac{260}{81}a+\dfrac{280}{81}b-\dfrac{10}{9}c+\dfrac{10}{3}d \\
\end{aligned}$
Suy ra $-\dfrac{260}{81}a+\dfrac{280}{81}b-\dfrac{10}{9}c+\dfrac{10}{3}d=\dfrac{250}{81} \left( 4 \right)$.
Từ $\left( 1 \right),\left( 2 \right),\left( 3 \right),\left( 4 \right)$ ta được $a=\dfrac{3}{20},b=-\dfrac{7}{20},c=-\dfrac{1}{10},d=\dfrac{7}{5}$.
Vậy $f\left( x \right)=\dfrac{3}{20}{{x}^{3}}-\dfrac{7}{20}{{x}^{2}}-\dfrac{1}{10}x+\dfrac{7}{5}$. Khi đó $f\left( x \right)=\int\limits_{0}^{1}{\left( \dfrac{3}{20}{{x}^{3}}-\dfrac{7}{20}{{x}^{2}}-\dfrac{1}{10}x+\dfrac{7}{5} \right)}\text{d}x=\dfrac{61}{48}$.
Đáp án B.